Från gymnasiemattens första kurser fick vi lära oss hur ekvationssystem löses när två linjära funktioner skär varandra i en punkt. I denna lektion vill vi utvidga detta koncept då vi oftast inte kommer ha två linjer och skärningen ofta inte bara är i en enda punkt.
Skärning mellan två linjer
Två icke-parallella linjer som är definierade i har alltid en skärningspunkt någonstans. För att hitta den punkten ställs ett ekvationssystem upp med varje linjes normalekvation där variablernas värden ska beräknas. Detta kan göras genom substitutionsmetoden eller additionsmetoden. Då detta är ett område som berörts i gymnasiekurserna kommer vi inte gå igenom dessa.
Skärning mellan ett plan och en linje
Säg att vi har en linje och ett plan, definierat i , då kommer linjen inte kunna vara definierad i normalform utan måste vara beskriven genom parametrarform.
Planet är vanligtvis definierat på normalformen . De eventuella skärningspunkterna kan uppstå i tre olika former:
Linjen är parallell med planet och ligger inte i planet: inga skärningspunkter
Linjen är parallell med planet och ligger i planet: oändligt med skärningspunkter
Linjen är inte parallell med planet: en skärningspunkt
För att beräkna eventuella skärningspunkter görs en insättning av linjens ekvation för varje variabel in i planets ekvation på följande vis
därefter använder planets ekvation för att göra en insättning av och
till sist är det bara att beräkna uttrycket och tolka resultatet. Precis som tidigare kan bara tre olika resultat uppstå efter förenkling:
Att vi får samma värde i både höger- och vänsterled, t.ex. : Oändligt med skärningspunkter
Att vi får olika värden i höger och vänsterled, t.ex. : Ingen skärning alls
Att vi får ett specifikt värde på , t.ex. : En skärningspunkt
Övning
Beräkna eventuell skärning som kan uppstå mellan linjen:
och planet .
Lösning
Vi börjar med att skriva om linjens ekvation som
och fortsätter med insättning av , och in i planets ekvation
Detta ger att linjen skär planet då , vi gör därför en insättning av värdet in i linjens parameterekvation:
Detta ger oss att linjen skär planet i punkten .
Skärning av två plan
Säg att vi har två plan i som är icke-parallella, då kommer deras skärning att vara en linje.
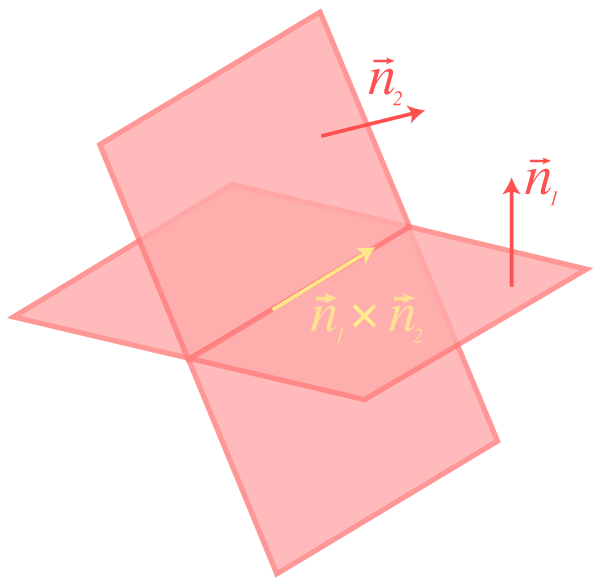
Denna linjes riktningsvekor är ortogonal mot båda planens normalvektorer. Tack vare detta kan vi beräkna linjens riktningsvektor genom att använda kryssprodukten.
Säg att vi har två plan:
Då kommer normalvektorerna för respektive plan att vara
Genom att använda kryssprodukten kommer vi få en ny vektor som är ortogonal mot de båda vektorerna. Denna nya vektor är linjens riktningsvektor. Vi kallar denna för :
När detta är gjort behöver vi bara en punkt som ligger på linjen för att kunna beskriva skärningen. Detta görs genom att hitta ett , vilket som helst som satisiferar ekvationsystemet för planen
Denna punkt kan vara vilken som helst och därför kan vi försöka gissa sig fram till denna så gått det går.
Övning
Finn skärningen mellan planen: och .
Lösning
Vi vet att skärningen måste vara en linje på formen och inleder därför med att ta reda på riktningsvektorn för skärningslinjen genom att ställa upp planen som ett ekvationssystem:
Vi vill nu använda planens normalvektorer och för att beräkna riktningsvektorn för skärningslinjen. Från planens normalekvation ges att
Vi använder nu kryssprodukten för att ta fram riktningen för skärningslinjen:
Vi har nu beräknat riktningsvektorn för skärningen. Vi vill nu hitta punkten . Vi söker vilket som helst som satisfierar ekvationsystemet
För att göra detta kan man gissa sig fram till ett eller räkna fram ett. Eftersom vi inte kommer på något bra att gissa på bestämmer vi oss för att använda additionsmetoden för att få fram ett enklare ekvationssystem som är mer gissbart.
Eftersom vi söker vilket som helst sätter vi och beräkna vad och borde vara. Vi får att och . Vi har därmed hittat en punkt som ligger i skärningen.
Avslutningsvis ger detta oss skärningslinjen för planen