Inledning
I gymnasiematten fick vi bland annat lära oss två begrepp: Definitionsmängd och Värdemängd. Definitionsmängden beskriver för vilka som värdet på funktionen är definierat som uttrycks som ett intervall . Värdemängden motsvarar då det intervall som ett värde finns för funktionen och uttrycks med:
Syftet med denna inledning är att inse att båda dessa mängder, definitionsmängden och värdemängden, har varit tallinjer hittills. I denna kurs kan mängderna vara allt från en punkt till en kub. (Teoretiskt kan mängderna vara större i dimension än en kub, dock förekommer det inte i denna kurs).
Delrum
Synonymer: Underrum, Subspace
Ett delrum kan liknas till en delmängd förutom att delrum dessutom har tre kriterium som måste uppfyllas. Så att vi har ett för att en delmängd ska vara ett giltigt delrum gäller följande:
Skalär multiplikation sluten: Om vektorn innehålls i så att , då måste där också vara innehållen i så att .
Vektoraddiditon sluten: Om vektorerna och innehålls i så att så måste också vara en vektor som är innehållen i så att .
Nollvektorn innehållen: Nollvektorn (eller origo) måste vara innehållen i så att .
Om alla tre kriterierna satisfieras samtidigt är delmängden också ett delrum. Delrum kan därför visualiseras genom geometriska form (punkt, linje, plan, kub, ...) som dimensionen för spannet ger upphov till samt att varje dimension är oändlig i sin egna riktning. Av denna anledning är alla linjära funktioner som skär origo delrum då deras linjer inte är ändliga samtidigt som de satisfierar den slutna vektoradditionen.
Bild
Synonymer: Bildrum, Kolonnrum, Image, columnspace
Kan liknas till värdemängd fast för transformationer
Tänk att vi har en linjär transformation . Då kan vi se att det enda som egentligen kan påverka transformationen är transformationsmatrisen . Det är därför rimligt att påstå att är det enda som kan påverka den bild (tänk värdemängd) som kommer uppstå av transformationen .
Sambandet mellan transformationsmatrisen och bilden är att det är kolumnvektorerna i är det som utgör spannet för bilden.
Man kan därför tänka sig sambandet mellan bild och transformationer på följande vis:
En vektor påverkas genom en transformation så att den transformeras till en ny vektor . Den nya vektorn måste därför vara innehållen i bildens spann då kan ses som en av bildens vektorer (eller ett värde i värdemängden). Detta kan illustreras på följande vis:
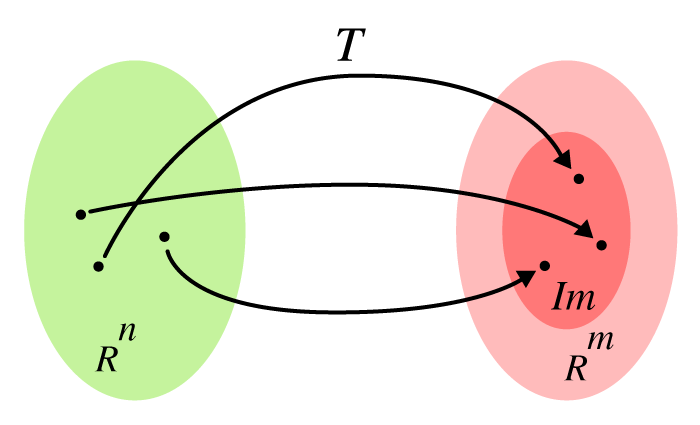
För varje värde i vår domän kommer det finnas ett värde som ligger i bilden (som är ett delrum till mål-domänen) som kan transformeras till genom transformationen .
Detta betyder ekvivalent att det inte är möjligt att ta ett värde i domänen, transformera det, och få ett värde utanför bilden. Transformationsmatrisen kommer inte göra det möjligt.
Om vi då har transformationen en transformationsmatris så kommer bilden att definieras av spannet av kolumnvektorerna så att . Detta kan tolkas som att kolumnvektorerna spänner upp bilden. Detta vill säga, om alla tre är linjärt oberoende kommer spannet att motsvara (eller en oändligt stor kub). Om två vektorer är linjärt oberoende kommer spannet motsvara (eller ett oändligt långt plan). Bilden därför kan tolkas som alla möjliga vektorer transformationen kan ge upphov till.
Kärna
Synonymer: Kernel, Nollrum, Nullspace
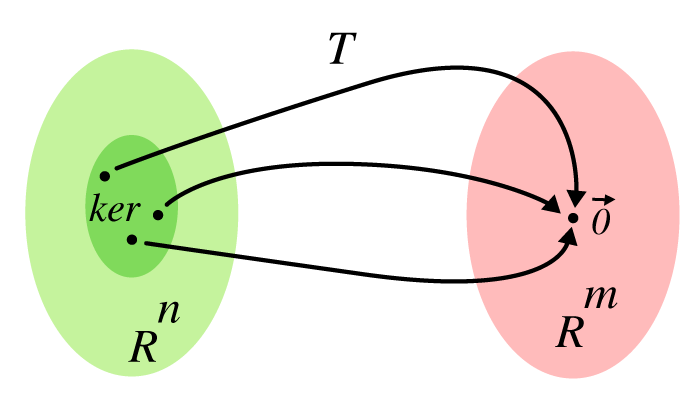
Tänk att vi har en linjär transformation där vi kräver att den vektor som ska transformeras till måste vara nollvektorn så att . Då kommer detta ge: där alla domän-vektorer transformeras till nollvektorn kommer satisfiera ekvationen. Dessa domän-vektorer kommer tillsammans att bilda en delmängd(och även ett underrum) av den totala domänen och kommer kunna definieras av spannet som uppstår av de vektorer som fås genom att beräkna rad-reduktionen av transformationsmatrisen. Detta spann kallas kärnan och beskrivs som där fås genom .
Till skillnad från bilden (som är ett delrum av mål-domänen) är kärnan ett delrum av domänen där alla vektorer innanför delrummet kommer alla att transformeras till nollvektorn (eller origo). Detta kan illustreras på följande vis: