Addition och subtraktion för vektorer fungerar likt skalärer men för de andra två räknesätten finns väldigt stora skillnader.
Det finns olika sorters multiplikation och men bara en division. De olika multiplikationerna beror på vad som multipliceras och påverkar utresultatet av multiplikationen. Vi har:
Vanlig multiplikation:
Skalärprodukt:
Kryssprodukt:
Matrismultiplikation
Då vi ännu inte har behandlat matriser ännu kommer den typen av multiplikation inte tas upp i denna lektion.
Multiplikation mellan skalär och vektor
Den vanligaste multiplikationen som förekommer är den mellan skalärer och vektorer. Om och är en skalär så kommer produkten av dessa vara:
Denna typ av multiplikation påverkar enbart vektorns längd som skalas upp eller ned gånger.
Övning
Vi har vektorn beräkna om
Lösning
Vi får
Skalärprodukt
Skalärprodukten beräknar vinkelförhållandet mellan två vektorer och betecknas på följande sätt och läses "u skalärt v". Resultatet av skalärprodukten är en skalär. Vi har vektorerna och så kommer deras skalärprodukt ges av:
Då detta har med vinklarna att göra finns det ett antal saker att ha i åtanke om resultatet:
Om är vektorerna vinkelräta mot varann
Om bildar vektorerna en trubbig vinkel
Om bildar vektorerna en spetsig vinkel
Övning
a) Beräkna skalärprodukten av och .
b) Bestäm om och är ortogonala (vinkelräta).
Lösning
a) Vi utför skalärprodukten
b) Då vet vi att vektorerna inte är vinkelräta mot varann.
Kryssprodukt
Denna form av multiplikation beräknar den vektorn som är vinkelrät mot de två vektorer som multipliceras genom kryssprodukten. Säg att vi har två vektorer, och då kommer kryssprodukten av dessa betecknas där är kryssprodukten och läses "a kryss b"
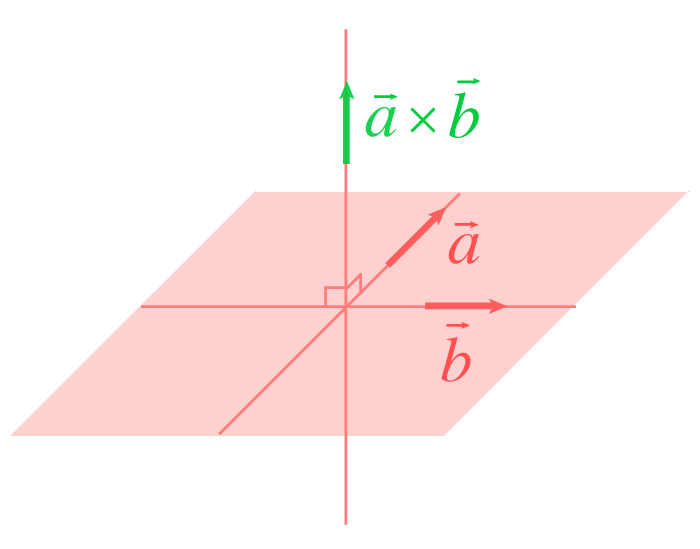
För att räkna ut kryssprodukten används formeln
Det finns även ett specialfall: Om och är parallella kommer
Kryssprodukten är dock bara definierad i .
Övning
Vi har två vektorer givna, och .
a) Beräkna deras kryssprodukt,
b) Avgör om vektorerna är parallella.
Lösning
a) Vi beräknar kryssprodukten:
b) Vektorerna och är inte är parallella då .
Normen
Normen av en vektor betecknas och motsvarar vektorns längd. Om så ges dess längd så att
Övning
Beräkna normen till vektorn som går från till .
Lösning
Först skapar vi vekorn där
Sedan applicerar vi formeln för att få vektorns längd:
som ger oss ,