Projektion
Säg att vi har två vektorer , och att vi vill återskapa i riktningen för . Då kan vi använda projektion!
Om vi projicerar på kommer resultatet av projektionen kunna betecknas och kunna betraktas som skuggan av vektor på . Detta kan illustreras som
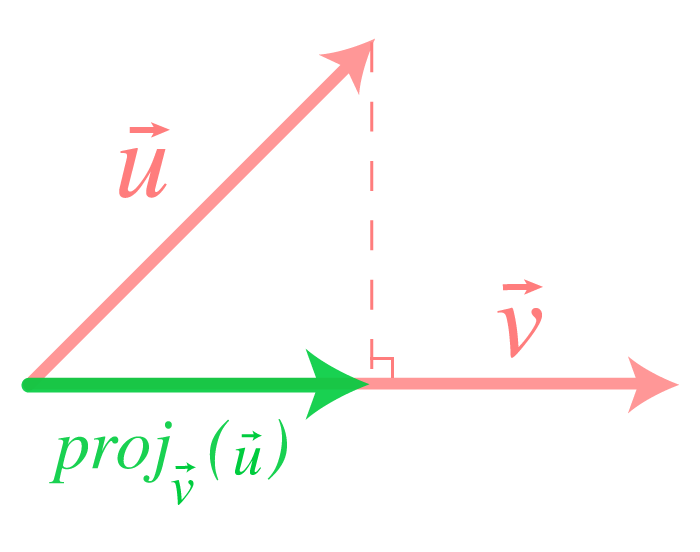
Den nya vektorn blir därmed parallell med den vektor som var målet för projektionen.
Formeln för projektion har utseendet
Notera att i formeln är vektorn som är målet för projektionen viktigare än vektorn som faktiskt projiceras.
Notera även att det är skalärprodukt mellan och , dvs
Övning
Vi har vektorerna
beräkna projektionen av på .
Lösning
Projektionen av på motsvarar . Detta kommer att ge oss
som avslutningen ger oss projektionen .
Reflektion
Säg återigen att vi har två vektorer och och att vi vill använda som en spegel för . Då kan vi använda reflektion.
Att reflektera längs betecknas och kan illustreras som
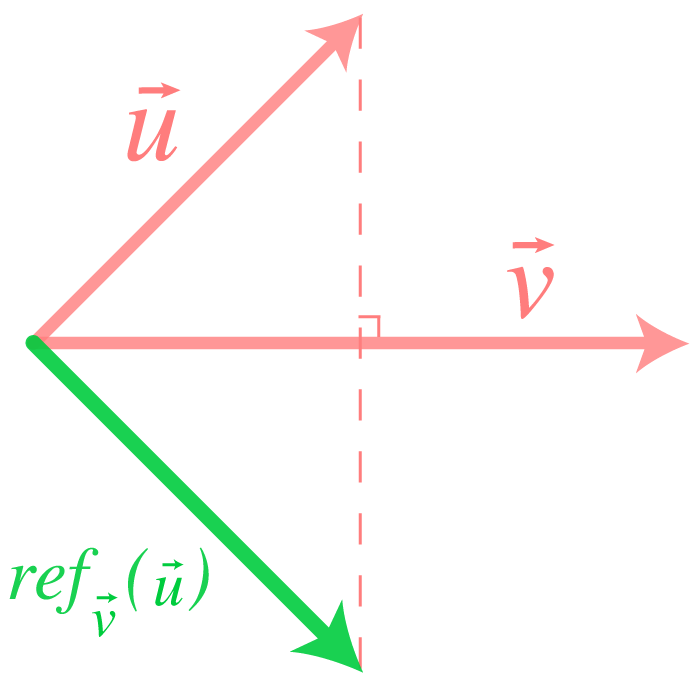
där formeln för reflektion ges av
Övning
Vi har vektorerna
beräkna
Lösning
Då vi vet formeln för reflektion, börjar vi med att beräkna projektionen och får projektionen till
och avslutningsvis reflektionen till
Vi har därmed skapat en vektor som är en spegling av längs