Matriser
Matriser är datahållare. De innehåller information som vi vill manipulera på olika vis. Alla matriser innehåller ett visst antal rader och kolonner som beskriver storleken på en matris.
När man anger storleken på en matris skriver man alltid: . Detta innebär att är ett exempel på en matris.
Om antalet rader motsvarar antalet kolumner så har man en kvadratisk matris: råkar vara en kvadratisk matris.
Matriser och transponering
Transponering innebär att raderna och kolumnerna i en matris byter plats. Transponatet till matrisen betecknas . Nedan finner vi ett exempel på hur en matris och dess transponat kan se ut
Addition och subtraktion
Att addera och subtrahera mellan matriser fungerar på ett väldigt intuitivt sätt. Den enda förutsättningen är att båda matriserna är av samma storlek. Både i antalet rader och kolonner.
Säg att vi har matriserna och som uttrycks av
då kommer additionen och subtraktionen se ut
Exercise
Vi har matriserna
a) Beräkna
b) Beräkna
Solution
a) Vi utför beräkningarna och får
b) Vi utför beräkningarna på samma vis som ovan och får
Skalär multiplikation
För att multiplicera en skalär med en matris så kommer resultatet att bli multiplicerat med varje element i matrisen
Viktigt!
Denna typ av multiplikation får inte misstas för skalärprodukten som är definierad enbart för vektorer där
Exercise
Vi har matrisen . Beräkna
Solution
Vi får till
Matrismultiplikation
Denna typ av multiplikation skiljen sig från mängden. Det kan betraktas så att varje rad i den första matrisen ska tas skalärt(Se skalärprodukten) med varje kolumn i den andra matrisen. Vart resultatet hamnar motsvarar vilken rad och kolumn som skalärprodukten utförs med.
Om vi har två matriser: och , så är multiplikationen inte densamma som , det vill säga: . Av denna anledning är det viktigt att hålla reda på vilken matris som är var.
För att multiplikationen av två matriser ska vara definierad måste den första matrisen ha lika många kolonner som den andra matrisen har rader. Detta illustreras på bilden nedan.
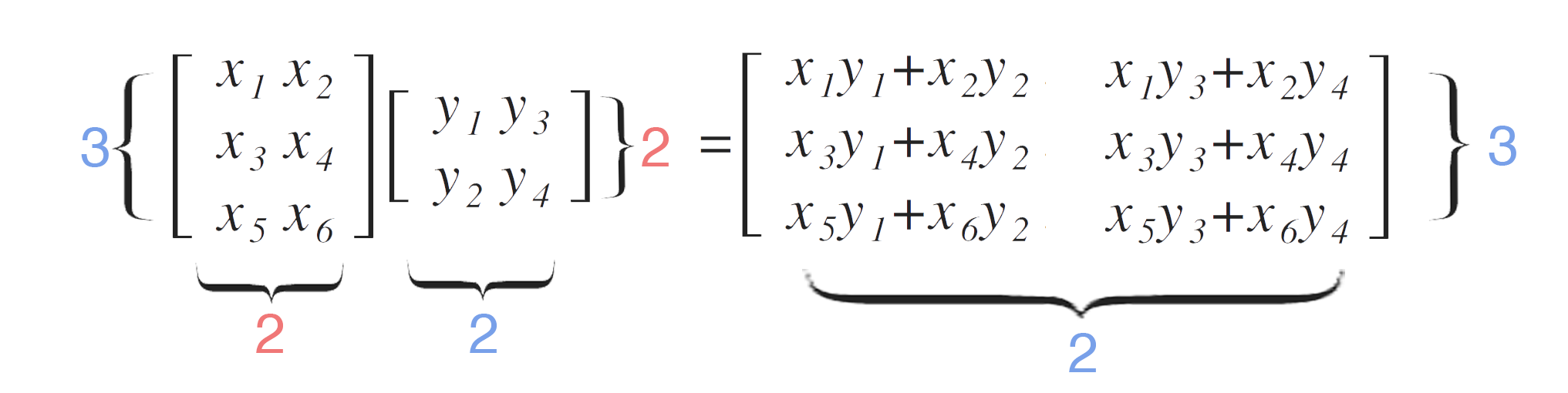
En sak som matrismultiplikation verkligen skiljer sig från andra operationer är att den inte är kommutativ, det vill säga att Om vi har matriserna och så gäller
Detta beror två saker
Beroende på antalet rader och kolumner i matriserna kan matrismultiplikationen inte längre vara definierad i t.ex men fungerar utan problem som .
Om multiplikationen faktisk är definierad kommer de att ge olika värden
Övning
Vi har matriserna
a) beräkna
b) beräkna
c) jämför resultatet från a) och b)
Solution
a) Vi börjar med att ställa upp multiplikationen
och ser att multiplikationen är definierad på antalet kolumner i den vänstra matrisen motsvarar antalet rader i den högra matrisen . Vi ser även att resultatet måste bli en matris eftersom den första matrisen har rader och den andra matrisen har kolumner.
Vi räknar ut
b) Vi fortsätter nu med att beräkna
och ser att resultatet måste vara en matris. Vi beräknar till
c) Vi ser nu tydligt att eftersom