Minsta kvadratmetoden används för att approximera lösningar till ekvationssystem som inte har några lösningar på grund av att de har ett för stort antal ekvationer.
Till exempel, ekvationssystemet består till exempel av tre linjära funktioner som inte alla tre skär någon punkt samtidigt, detta gör att systemet i sig saknar lösning.
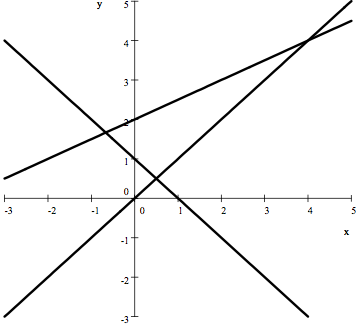
Minsta kvadratmetoden ger oss möjligheten till att beräkna den närmaste lösningen, punkten som är närmast de tre linjernas skärningspunkter.
Det går till genom att ha ett ekvationssystem som uttrycks som en linjär transformation och sedan förlänga både vänster och högerled med så att man får ekvationen
Detta kommer göra att vektorn kommer bli den approximerade lösningen av systemet!
Övning
Beräkna en minsta kvadratlösning till ekvationssystemet
Lösning
Vi börjar med att skriva upp ekvationssystemet uttryckt som en linjär transformation
Vi kallar matrisen i vänsterledet för , vektorn i vänsterledet för och vektorn i högerledet för så att
Vi tar därefter fram transponatet för som kan uttryckas som
Vi multiplicerar därefter i både högerledet och vänsterledet i ekvationen så att vi får:
detta ger oss ekvationen
vi utför matrismultiplikationerna och ställer upp det i en totalmatris
Och använder sedan Gauss-Elimination för att få matrisen i trappstegsform
Detta ger oss lösningen