Spolars strömändringar och motorers temperaturändringar har väldigt snarlika funktioner. Jag tänkte därför att vi kunde försöka komma på en generell formell som sammanfattar transienta förlopp, för att göra det enkelt att komma ihåg och förstå alladessa formler.
Låt oss därför hitta på en storhet som kan "laddas" och "urladdas" på samma sätt som de ovan, vars ursprungsvärde är . :s förädingstakt beror på dess tidskonstant , som man får fram genom att lösa differentialekvationer som beskriver situationen. För kondensatorns spänning gjordes detta med hjälp av omskrivningar av Kirchhoffs lagar.
Om vi nu i vårt påhittade fall skulle börja "urladda" skulle den sjunka ner mot med en takt som beror på vårt . Ekvtionen skulle se ut som:
Om vi nu skulle "ladda" med någonting, så borde öka tills den nått det slutvärdet som den laddande parten har. Vi kallar därför det värdet: . ser då ut såhär:
Båda fallen kan då sammanfattas med denna graf:
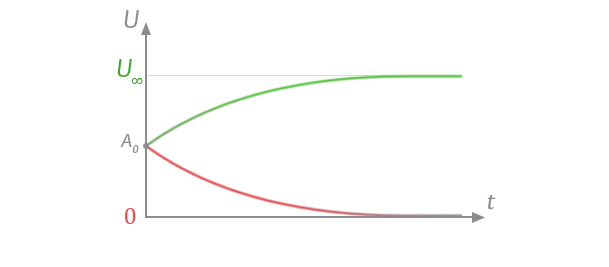
Så om ni har svårt att komma ihåg alla 3 formler, tänk tillbaka till dessa två.
Som ni kan se beror utvecklingen av helt och hållet på begynnelsevärdet och tidskonstanten . Om nu skulle inte variera, utan bara sitta på . Om skulle stanna kvar på det värdet. Ju större är, desto långsammare sker förändringen, och vise versa.