Hur dessa storheter utvecklas kan man beskriva med väldigt snarlika formler. Låt oss börja med att titta på en kondensator.
Kondensatorer
See errorId 3

Vi är intresserade av kondensatorns "transienta storhet", dess spänning. I ekvationen ovan förekommen dock även ström. Strömmen kan också variera med tiden, men vi vill uttrycka den med i stället. Som tur är gäller det att
Tidsderivatan av laddningen är ju helt enkelt "laddningsflödet", med andra ord strömmen , vilket betyder att
Om vi sätter in detta i vår första spänningsekvation får vi: och till slut
eller
Låt oss fundera på den här ekvationen en stund. Om är spänningen i kondensatorn, så borde den ju vara , och förbli , i med att kretsen varit i läge under en lång tid. Kondensatorn måste därför vara helt urladdad och då den inte får någon mer ström.
Som ni kanske redan märkt så kan inte vara en enhetslös konstant. För att denna ekvation ska vara korrekt måste vara en tidsenhet. Det är nämligen så att RC är kondensatorns tidskonstant, som man bettecknar . Detta gäller för alla kondensatorer.
Det här fallet var dock rätt tråkigt, kondensatorn har ju ingen laddning. Hur skulle det se ut om den hade det? Hur skulle det se ut om ? Låt oss säga att vi precis slagit om till läge i stället, och att kondensatorn då har en spänning . Vi kommer då att bevittna:
med vilken vi kan avgöra hur spänningen i kondensatorn kommer variera. Vi har just nu att:
Urladdning
i H.L. Därefter integrerar vi båda leden:
See errorId 4
Om ni kommer ihåg denna sorts funktion från diffen eller fysiken så kanske ni minns att konstanten bestämms med hjälp av begynnelsevillkoren. Det är nämligen så at att vid så är , vilket betyder att . är nämligen vårt begynnelsevärde. Vi får då:
Som ni kanske redan anar från hur denna funktion ser ut så kommer att avta med tiden, tills den når , det är det så kallade slutvärdet. Ofta betecknar man detta som:
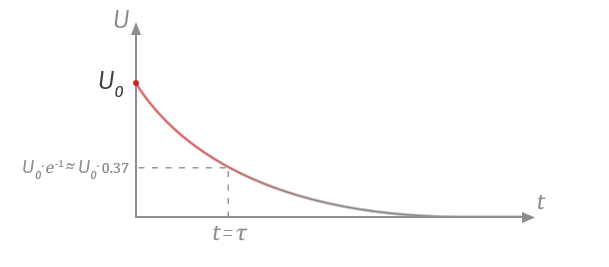
Som ni kan se så är tidskonstanten inte samma sak som halveringstiden. Då så har vi nämligen att .