Vridningskraft & Vridningsmoment
I mekanik säger man att ett föremål är i vila då summan av alla krafter som verkar på föremålet är 0, vilket man kan skriva som:
Men detta är inte det enda villkoret för att ett föremål ska vara i vila. Det får nämligen inte heller snurra. Problemet med uttrycken ovan är att de inte specificerar var dessa krafter appliceras.
Ta dessa två exempel:
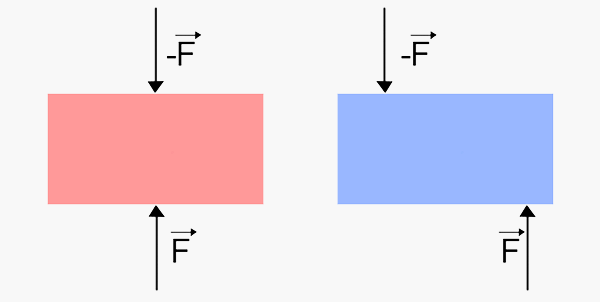
På lådor appliceras en kraft och dess "motsats" på ett objekt. I båda fallen är .
Alltså borde väl båda objekten vara i vila? Men så är det ju inte.
Intuitivt kanske ni redan märker att den blåa lådan kommer snurra, som så:
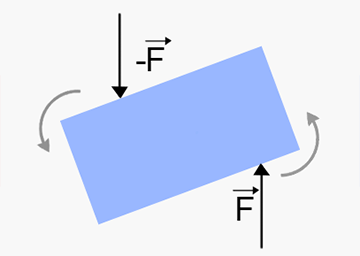
Alltså är detta föremål inte vila, trots att summan av alla krafter är .
Vi måste alltså även tänka på det så kallade vridningsmomentet. För att ett föremål skall vara i vila måste alltså dess vridningsmoment vara .
Man talar dock oftast inte om ett helt objekts vridningsmoment utan om vridningsmomentet i en punkt.
Hur tänker man alltså när det gäller vridningsmoment?
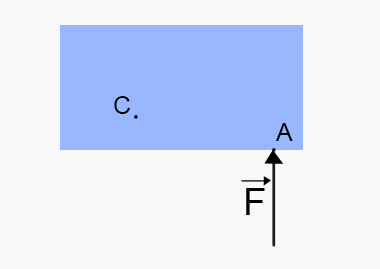
Ta lådan ovan. "vidrör" lådan i en så kallad angreppspunkt: . Om vi nu vill räkna ut vridningsmomentet i en punkt C ritar vi ut följande vektor.
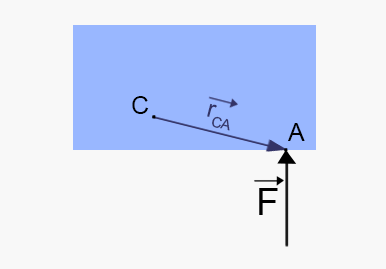
Tack vare denna vektor , samt vektorn , så vill vi få varat vridningsmoment.
(Varför skriver man och inte bara ?... bra fråga. Detta är bara en av flera knöliga beteckningar som används ofta. Båda kan användas (och är "rätt") eftersom det bara är namngivning som skiljer de åt. Det råkar bara vara så att många använder det. )
Vi söker alltså vridningsmomentet i en punkt som orsakas av att en kraft verkar på angreppspunkten . Detta får vi genom formeln:
Där är momentet i punkten .
Om ni har algebran fräscht i minnet kanske ni nu inser att den här kryssprodukten kommer ge oss en vektor.
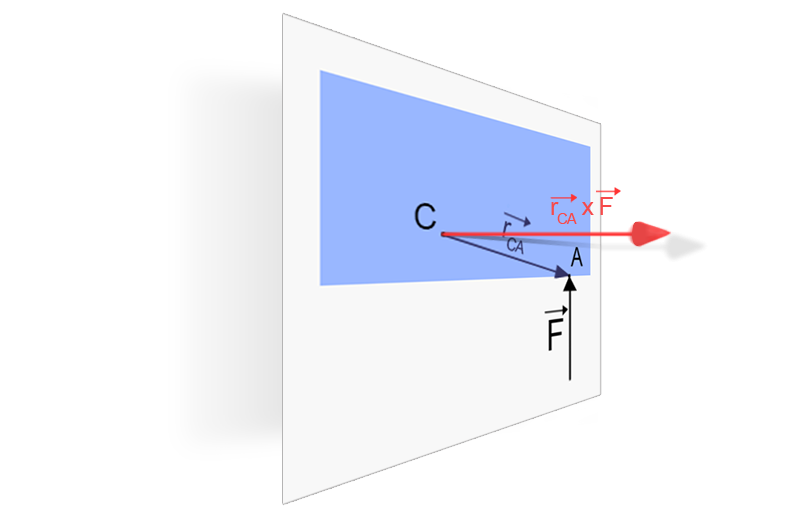
Vad är då denna vektor? Tänk igen på hur den hår lådan snurrade. Den snurrade moturs, alltså i positiv riktning (som i trigonometri).
Precis denna information har vi fått utav denna vektor, (cf. kryssprodukten från algebra), i med att den pekar utåt.
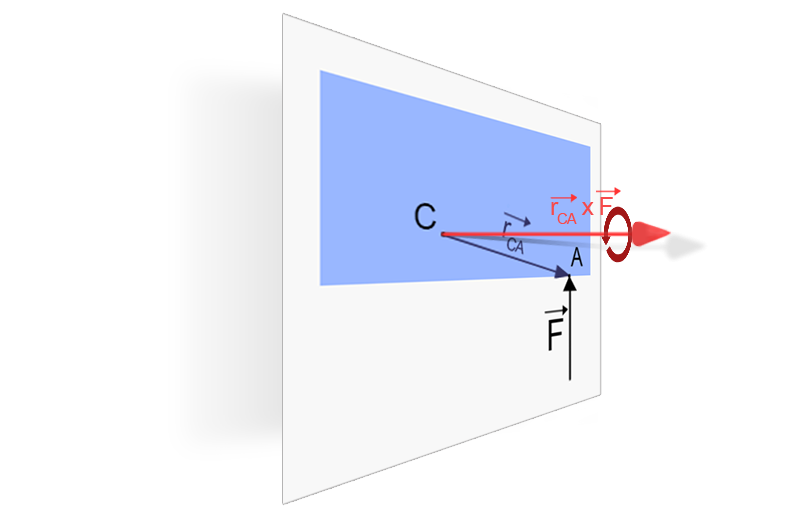
Om vi placerar i punkten C som ovan, får vi fram axeln kring vilken C roterar. Vektorns storlek visar dessutom hur stark denna vridningskraft är.
Vad vi fått ut är alltså både vridningens riktning </b>(moturs/medurs), axeln</b> den följer, och hur stark den är.
Låt oss ta det ett steg längre genom att anta att detta är ett så kallat plant problem.
Om och får vi från kryssprodukten att
Vridningskraften är alltså i detta fall :s storlek, med andra ord . Mer än så kan vi inte räkna på utan att ansätta några koordinater, men detta räcker gott till en början.