Inledning
Vårt klassiska koordinatsystem, det kartesiska systemet är tyvärr inte optimalt för att uttrycka en del funktioner, i första hand cirkulära funktioner. Att gå över till ett annat kordinatsystem kan ha fördelar i simplifiering utav uttryck, detta kommer till användning främst under integration där det annars kan bli inhumana arbetsförhållanden. Denna lektion syftar till att ge förståelse för variabelbyten i kombination av just integraler.
Man kan gå över till praktiskt taget vilket kordinatsystem som helst och till och med hitta på ett eget som talas vid länge ned. Det vanligaste variabelbytet man kan göra är till något typ av cirkulärt system.
Variabelbyte till cirkulära koordinater
Cirkulära koordinater finns i flera former, det som skiljer de år är den tredje dimensionen (det som vi vanligt kallar -led). De cirkulära kordinatsystemen är följande:
Polära koordinater
Elliptiska koordinater
Sfäriska koordinater
Cylindriska koordinater
De två första, polära och elliptiska koordinater är båda av dimension och har variablerna . Det som skiljer det polära koordinatsystemet mot det elliptiska är att variabeln varierar i värde i det elliptiska medan det är konstant i det polära koordinatsystemet.
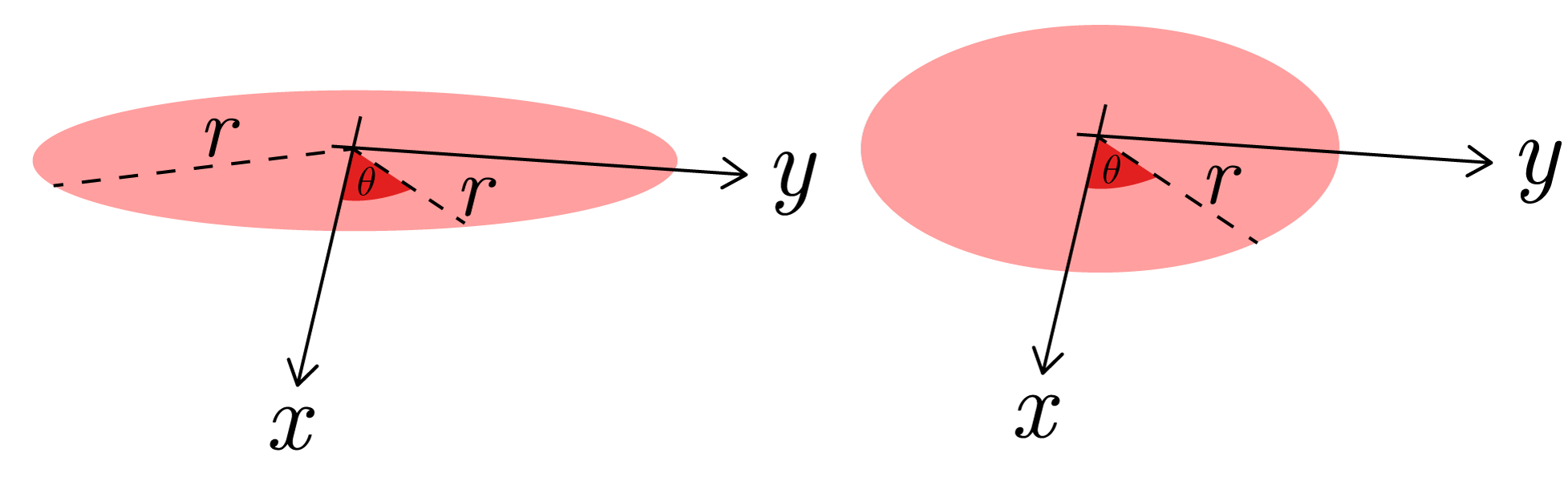
I denna kurs kommer vi även att använda oss av sfäriska och cylindriska koordinater som båda är av dimention . De har variablerna och respektive.
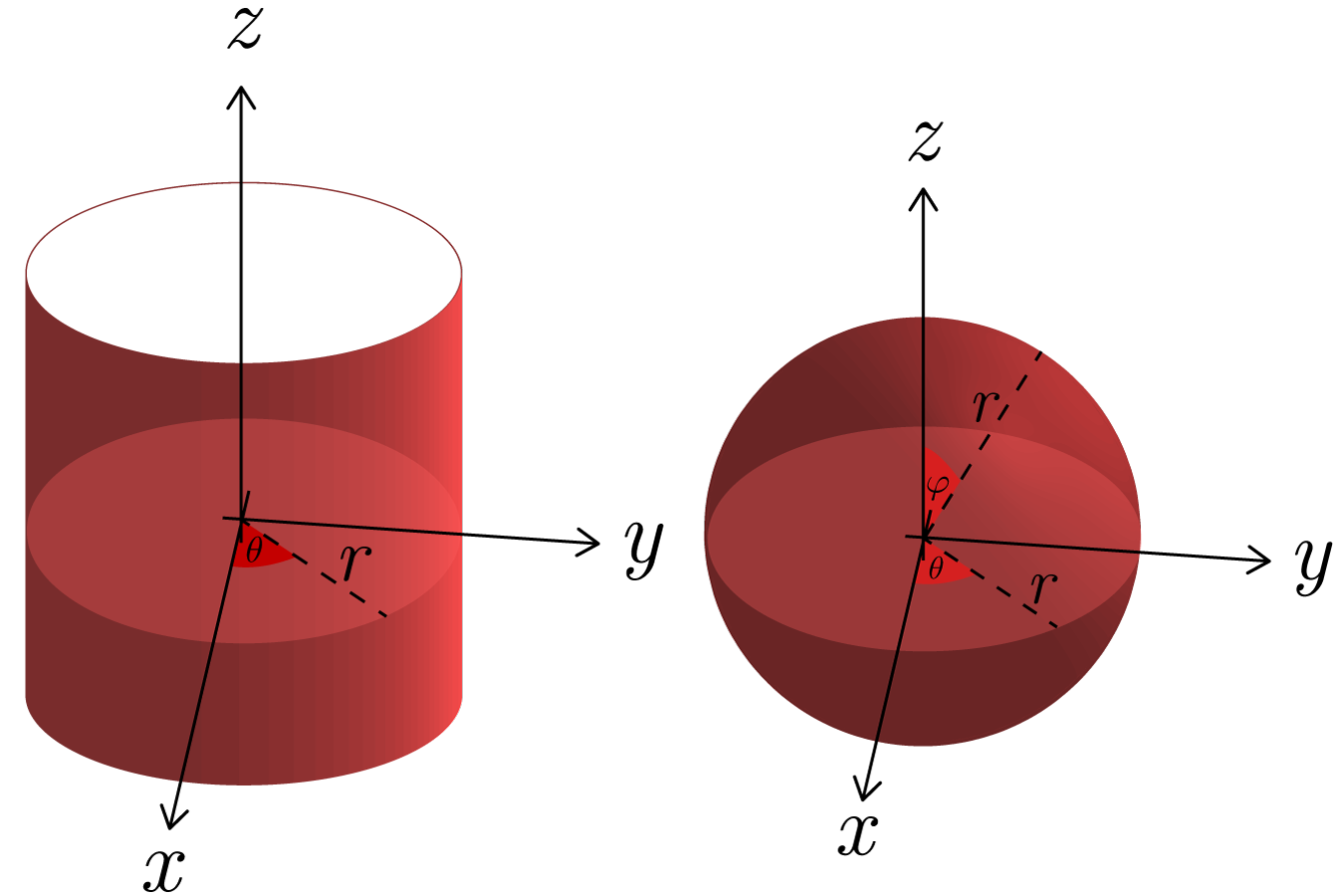
Vilket system som lämpar sig bäst beror helt på problemet i fråga. Nedan följer de variabelbytet från det kartesiska koordinatsystemet till det polära, cylindriska och sfäriska koordinatsystemet.
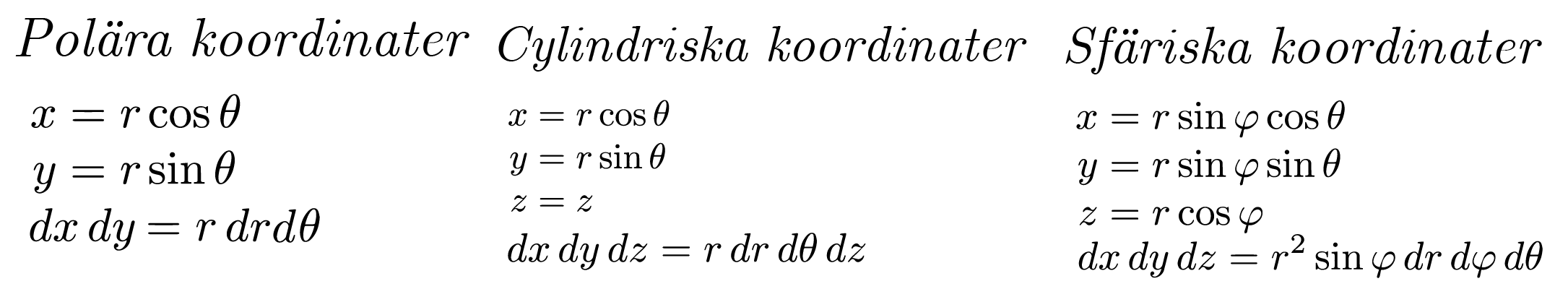
Notera: Att endast går från och inte då det räcker för att rita en hel sfär! Det blir då som en halvcirkel som ritas av och roteras runt med för att bli en sfär!
Eliptiska koordinater
Man kan även skapa elliptiska koordinater genom att ha ett och som representerar var ellipsen är centrerad. och är de värden ellipsen skär genom på respektive axel. Dessa kan analyseras genom formeln för en ellips (som likar cirkelns ekvation):
Genom detta kan man då få de eliptiska koordinaterna:
I allmänhet är de väldigt lika polära koordinater.
Då det bästa sättet att lära sig variabelbyten är att faktiskt utföra de kommer räkneexempel att behandlas i slutet av denna lektion.
Variabelbyte till valfria koordinater
Säg att vi har funktionen och vill integrera den över ett område där med avseende på och ger detta oss följande integral:
Vi vill nu utföra ett variabelbyte till , då måste vi även ändra så att vi integrerar över de nya variablerna istället. Detta görs med Jacobi determinanten som är en extra faktor till de nya variablerna
Notera att i Jacobi determinanten betraktas och nu som funktioner av och ! Det är av denna anledning vi har extra faktorer i när vi gör ett variabelbyte till de cirkulära systemen (där för sfäriska). Att beräkna Jacobin är inte svårt om man kan explicit förenkla vad och substitut blir. Detta gör vi i exemplen nedan.
Viktigt: Jacobideterminanten måste uppfylla följande villkor då annars variabelbytet inte är giltigt:
Integralen i sig har därför följande utseende efter variabelbyte
Notera: Området vi integrerar på påverkas utav variabelbyte då det är definierat av de tidigare koordinaterna. Detta innebär att vi måste omskriva vårt område till de nya koordinaterna. Vårt nya område uttryckt i -koordinater blir då och kan mycket väl ha en anna geometrisk form än då den är anpassad ett helt annat system.
Räkneexempel
Exercise
Beräkna Jacobi determinanten för variabelbytet
Solution
Vi använder oss utav definitionen för Jacobin och beräknar de partiella derivatorna. Sedan beräknar vi determinanten och bryter ut $$r$$ samt utnyttjar trig. ettan:
Detta ger oss att vilket stämer då det var polära koordinater bytte till.
Exercise
Beräkna då
Solution
Genom att analysera kan man se att det är en ellips. Vi utför en omskrivning av så att och inför därför koordinaterna:
Detta koordinatbyte ger Jacobianen
efter detta variabelbyte får vi nu att som ger oss gränserna för de nya variablerna samt . Vi beräknar nu integralen och får