Vridning är relativt simpel i praktiken, det följer nämligen en formel som sällan förändras. Vi tittar på en typisk uppgift som kommit på en tenta.
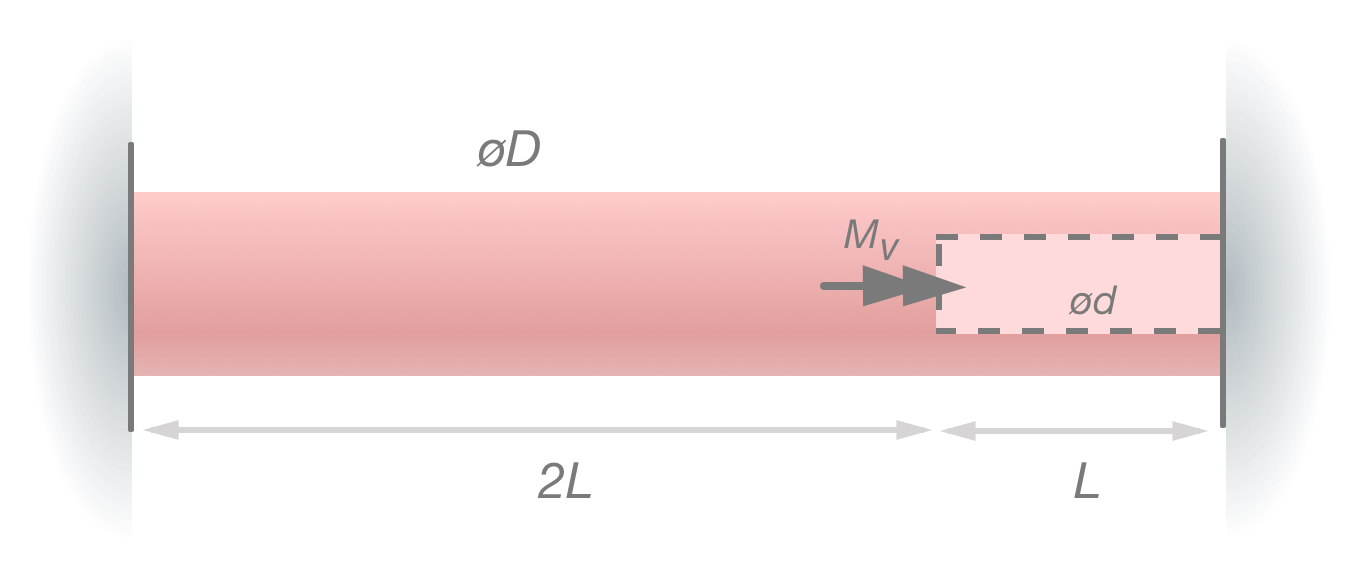
En axelkonstruktion, fast inspänd på båda sidorna, består av två delar: En lång homogen del med diameter , och en urborrad del med diametern , vars längd är . Ett vridande moment belastar axeln mellan dessa delar. Uppgiften ber oss ta reda på hur stort vridmoment som krävs för att orsaka fullplasticering.
Till att börja med måste vi ta reda på var den största påfrestningen sker, och hur stark den är, så vi kollar först jämvikten.
Jämvikt
Två reaktionskrafter från väggarna uppkommer, och vi får således , med andra ord ett statiskt obestämt problem. Som tur är kan vi nöja oss med detta. Full plasticering sker nämligen då båda bitarna plasticeras genomgående. Vi måste alltså ta reda på vilken kraft som krävs för att detta ska ske i vardera bit, och sen sumera de. Snittning gör detta ännu tydligare. Om vi skär upp axeln i 3 bitar, och bara kolla på den mittersta...
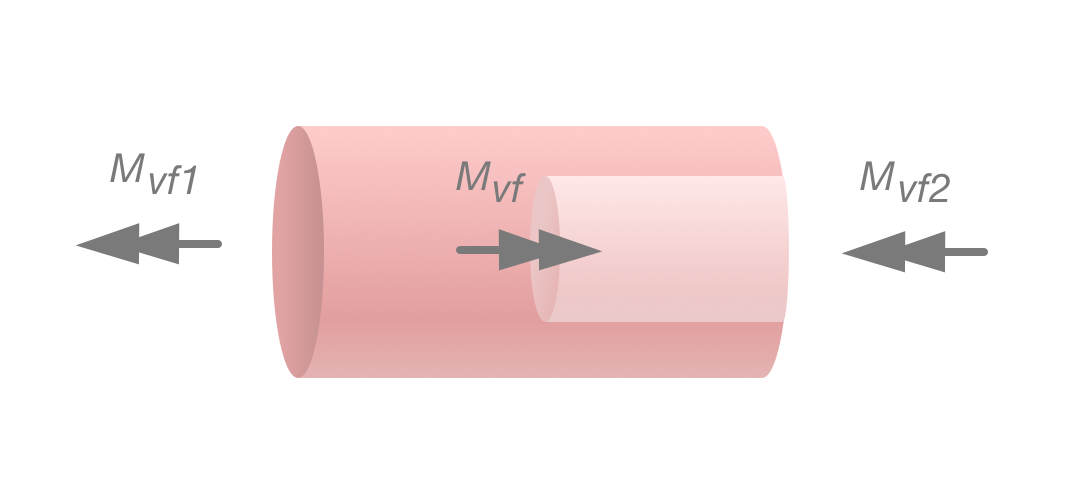
Så kan vi se att . De andra bitarna ger oss även enkelt att reaktionskrafterna och är lika stora som inre krafterna respektive
Snitt-jämnvikten stämmer alltså bra överens med våran första ekvation. Uppgiften informerar oss att plasticering sker vid . Nu räcker det bara med att tillämpa formeln
[F.S s.74]
Om vi sätter in parametrarna för varje del i den får vi:
För vänstra:
För högra:
Full plasticering alltså ske då , med andra ord då: