Vi börjar nu med en uppgift som tar upp både drag-, tryck- och böjspänningar i snittningen. En balk som representeras nedan belastas av en kraft , som angriper balken snett med en vinkel . Vi förväntas räkna ut vad största drag- respektive tryck-spänningen är i balken.
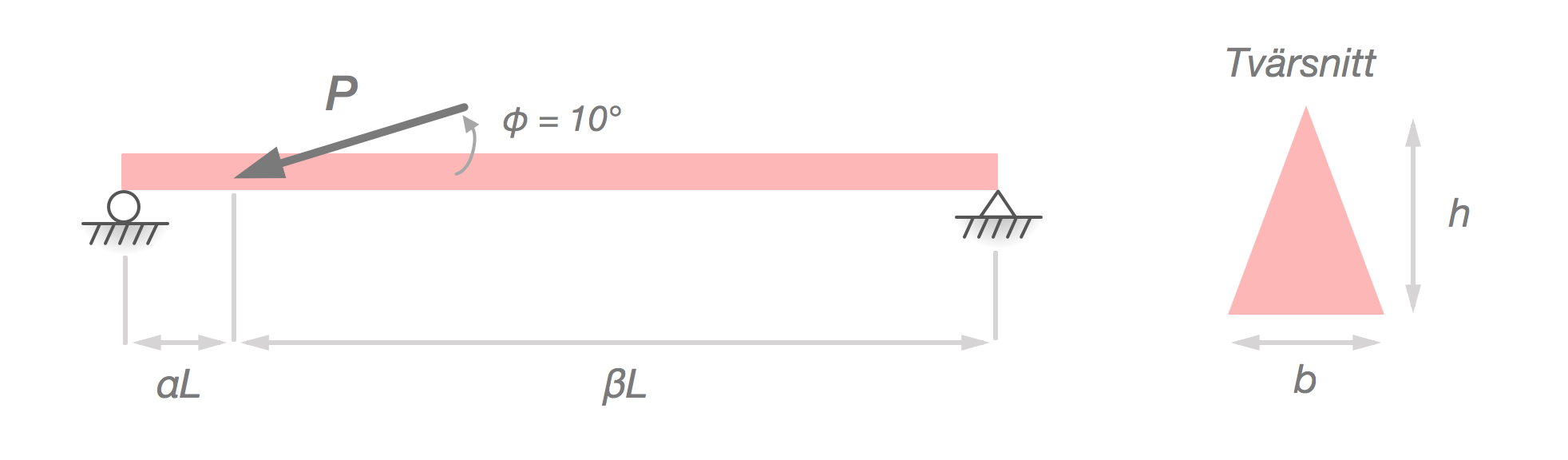
Givet har vi: °, , , och .
I - Jämvikt
För att vara konsekventa börjar vi med att ställa upp vad som krävs för att balken skall vara i jämvikt. I första hand delar vi upp till dess horisontella komposant och dess vertikala, , så att: och
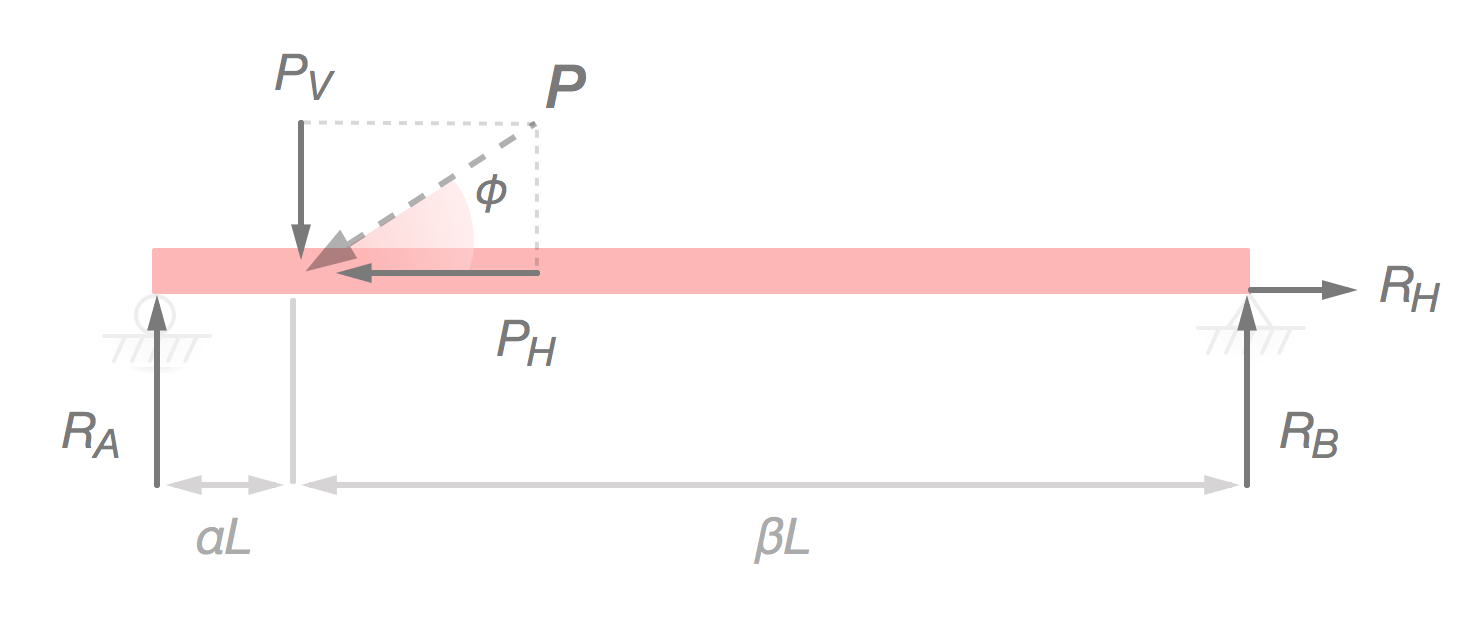
För att det ska gälla måste vi ha:
Från får vi då .
Insatt i blir det:
Om vi nu omvandlar komposanterna erhålls:
, och från :
II - Snittning
När man väl kommit igång såhär är det lätt hänt att man går börjar snitta för snabbt, och bara delar upp balken i tre bitar. Det kan då se ut såhär:
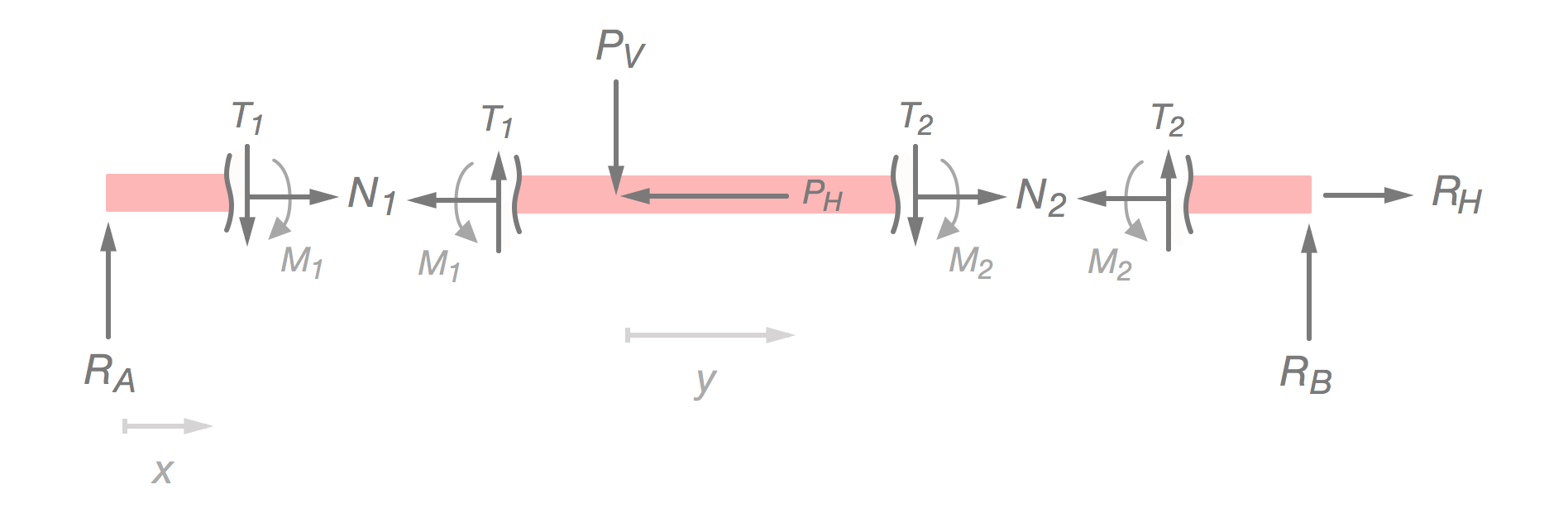
Somliga tycker kanske att det går att lösa på det här sättet, och det gör det... Men ni lär slita håret av er i processen och tappa viktiga minuter på tentan. Vad vi behöver lära oss är vad vi kan skippa och förenkla.
Tvärkrafterna kommer till exempel inte ha något inflytande på drag- eller tryckspänningar, så vi kan bortse från de.
Den vänstra ändpunkten är dessutom "på hjul". Detta gör att ingen tryck- eller dragspänning kommer att ske i balken mellan och angreppspunkten , så har inget inflytande här. Däremot kommer de böjspänningar som orsakar mellan punkten och att skapa drag och tryck spänning i tvärsnittets över- och underkant, som så:
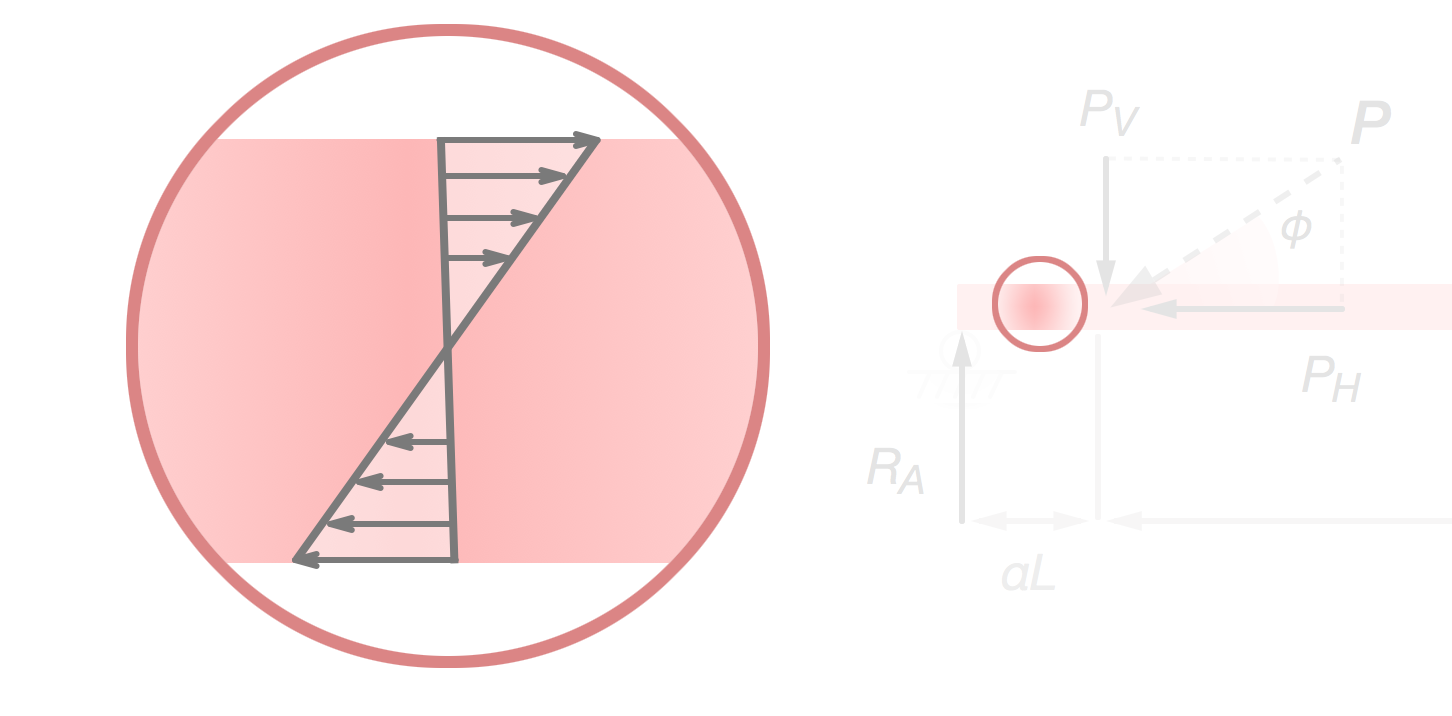
Samtidigt, mellan och så "drar" kraften i balken, i med att är fäst i marken. Därför kommer dragspänningar orsakas av och böjspänningar orsakas av . Dessa kommer bilda spänningar i balken som så:
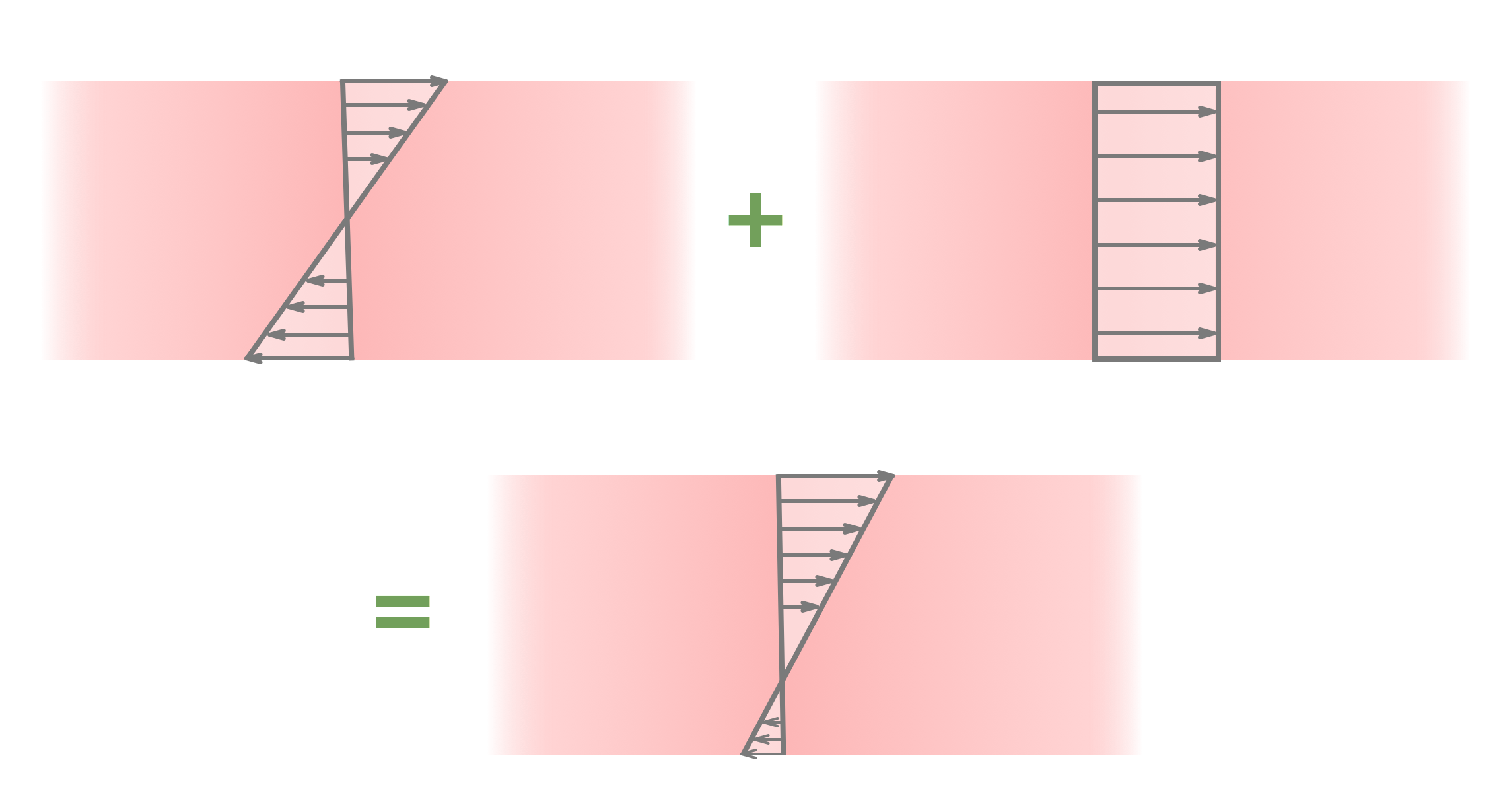
Nu när vi vet att båda sidorna av balken kan förenklas på varsitt sätt ska vi försöka använda det till vår fördel. Låt oss förstsnitta mellan och och ta den vänstra balkbiten.
Vänstra balkbiten
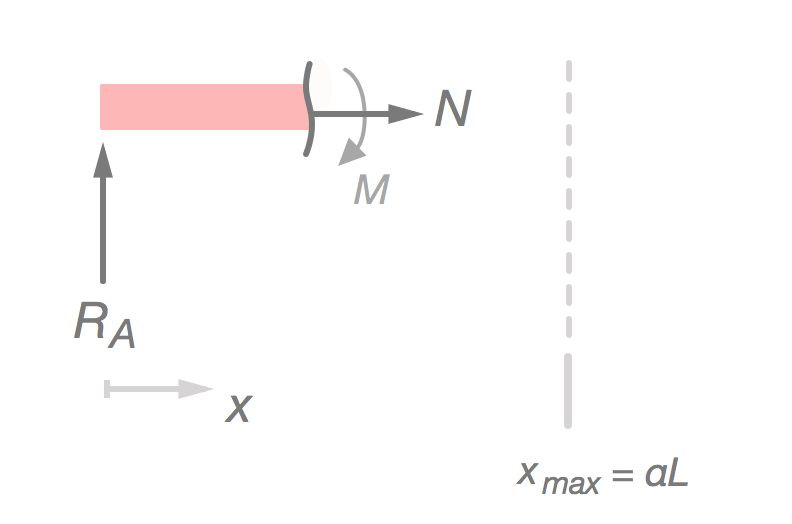
Låt . Då får vi:
Precis som vi sa innan är noll, det vill säga att det inte uppstår någon drag- eller tryckspänning i mitten av snittet. å andra sidan ökar med . Den är alltså maximal då , dvs . Nu när vi vet vad den maximala spänningen är, samt var i denna snittbit den befinner sig, så kan vi börja räkna. För att ta reda på hur böjmomentet inverkar på snittets över och underkant använder vi oss av ekvationen . är avståndet mellan tvärsnittets masscentrum och dess under-/överkant.
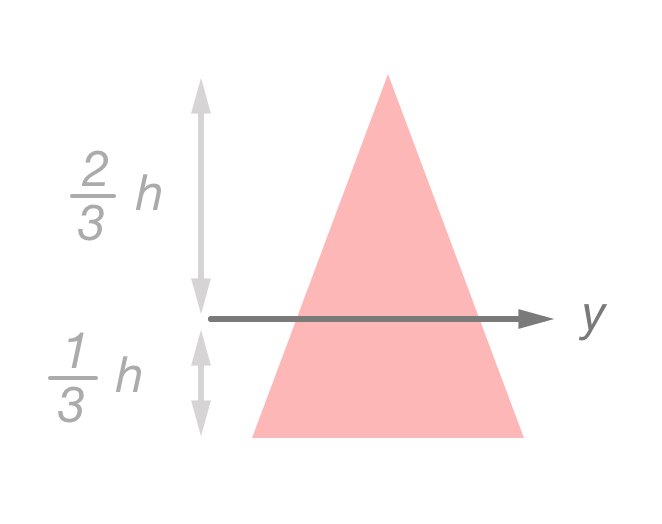
Alltså har vi att ("z överkant") är lika med och ("z underkant") är lika med ( är negativ eftersom man "förflyttar" sig neråt från masscentrum för att ta sig till underkanten). Dessutom gäller det att för detta snitt är:
Tillämpat till denna snitt-del får vi:
Notera att . Det betyder att och . Så ja, nu har vi halva arbetet gjort. Dags att ta oss an andra biten.
Högra balkbiten
Vi tittar nu på delen av balken mellan och . För att göra saker enklare och slippa komplicerade längduttryck väljer vi att byta riktning. Resulterande schemat blir:
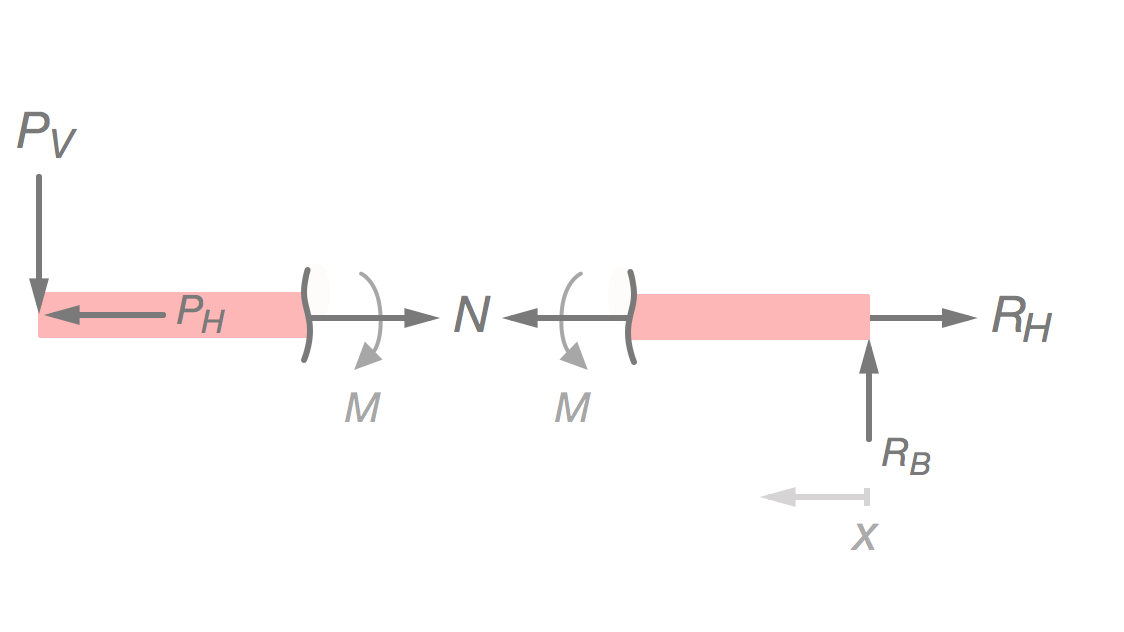
Fokusera på högra delen i bilden. För att jämvikt ska råda måste: och .
Som vi nämnde tidigare har vi alltså både en böjning och en axiell spänning (I med att så är det en dragspänning). Vi måste alltså summera denna normalkraft med den största böjspänningen. Som ni kan se i ekvationen för , så är den störst då . Med andra ord: . För att erhålla den totala spänningen i både över- och underkant använder vi oss av formeln: . Tvärsnittets area är helt enkel
Om vi nu precis som innan kollar på spänningen i över och underkant blir detta:
Det gäller även att . Alltså måste samt .
Svar
Vi kan nu se att de absolut största drag och tryckspänningarna känns kring angreppspunkt. är den största dragspänningen och är den största tryckspänningen. Om ni vill kan ni räkna ut och sätta in värdet gentemot kraften P, men eftersom vi redan definierat med avseende på ovan kan det kännas onödigt. Som ni kan se höll vi oss ifrån för jobbiga beräkningar genom att hålla oss till "bokstäver". Försök att inte ta fram tal för snabbt i uppgiften, eftersom det väldigt lätt blir bökigt.