Längden av en kurva
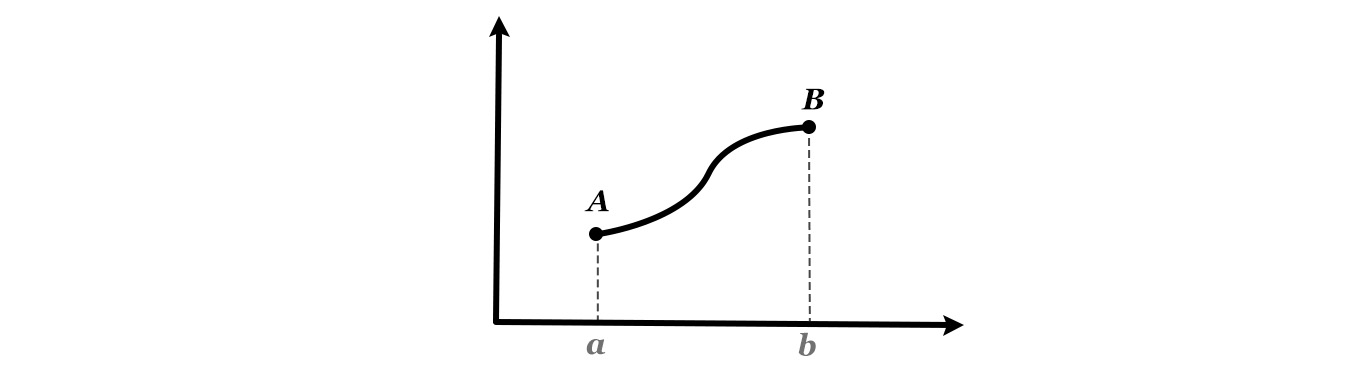
Om man känner till funktionen och vill räkna ut längden av funktionens kurva mellan punkterna A och B använder man formeln:
Eftersom formeln är väldigt enkel kommer vi att gå igenom ett lite svårare exempel som skulle kunna komma på tentan:
Uppgift
Beräkna längden av kurvan på intervallet
Lösning
Vi ska applicera formeln
Vi räknar först ut .
kan ses som följande sammansatt funktion:
, där och .
För att räkna ut dess derivata använder vi kedjeregeln:
Vi får de separata derivatorna och , alltså är:
Nu när vi har s derivata kan vi sätta in den i formeln för längden på en kurva:
(genom potensregeln för dubbla exponenter)
Längden på kurvan är alltså !
Area
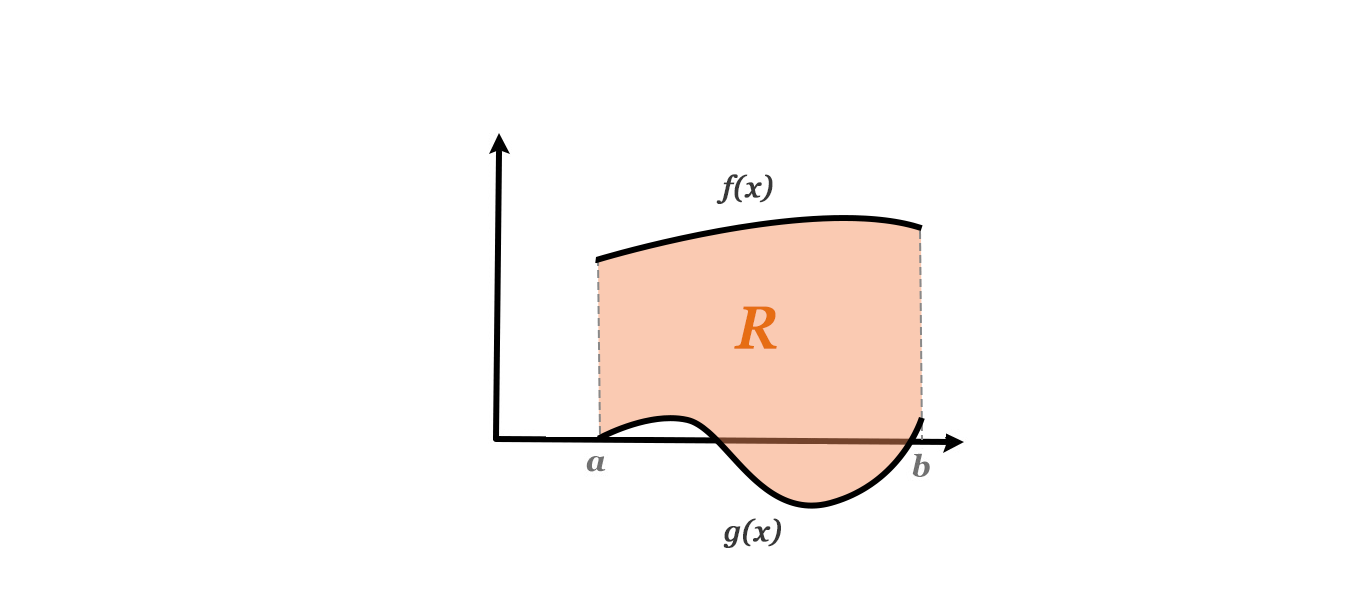
För att räkna ut arean till en yta som begränsas av två funktioner tar vi arean av den övre funktionen minus arean till den undre funktionen . Vi applicerar alltså formeln:
Uppgift 2
Beräkna arean av området som begränsas av kurvorna och
Lösning
Vi måste först beräkna skärningspunkterna mellan båda kurvorna. Vi sätter:
Vi får alltså och , vilket är intervallet för vår integral.
Vi måste nu veta vilken av funktionerna som är överst i det här intervallet. Vi tar därför ett slumpmässigt nummer i intervallet, t.ex. och ser vilket värde som får av funktionerna:
Eftersom vet vi alltså att i intervallet .
Vi kan nu applicera formeln:
Arean av området är alltså lika med
Rotationsvolym
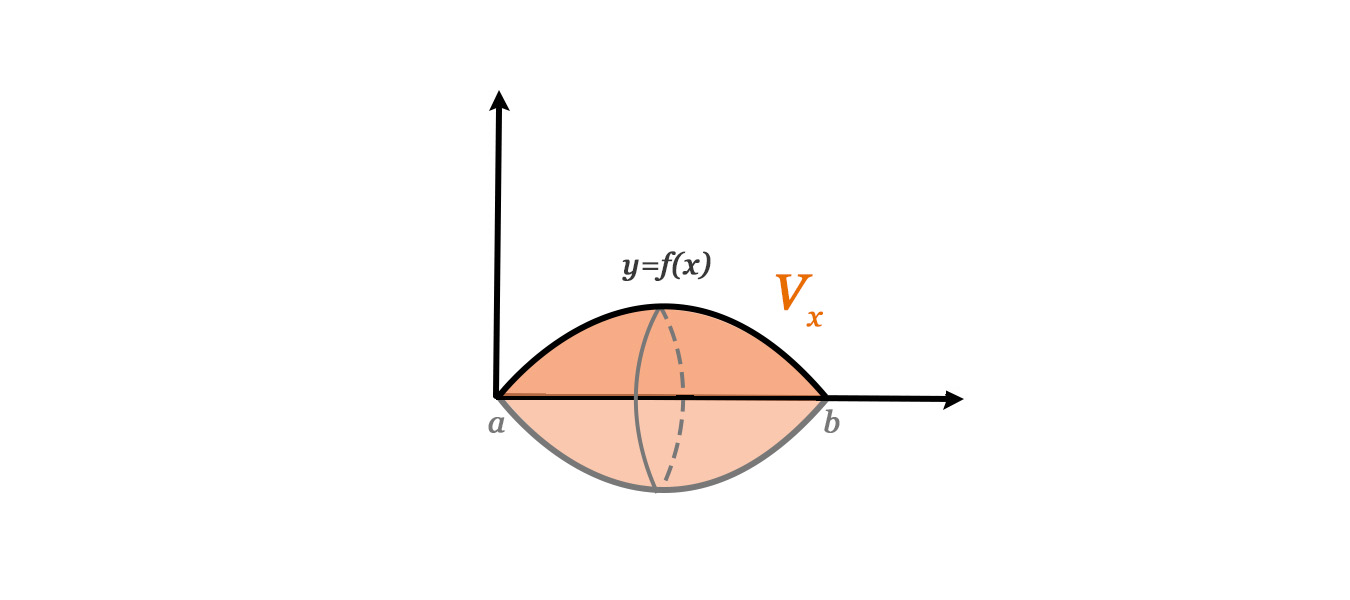
Om R är en area som definieras av funktionen , kan man räkna ut volymen som uppstår när:
R roterar kring x-axeln:
R roterar kring y-axeln:
Uppgift 3
Beräkna volymen av den kropp som fås mellan och genom att rotera kring -axeln.
Lösning
Vi applicerar formeln:
Vi gör en variabelsubstitution:
Kroppen har alltså volymen