Väntevärde
Av alla värden i utfallsrummet finns det ofta en del som händelsen oftare resulterar i. Väntevärdet är det förväntade utfallsvärdet borde ligga i närheten av och inte det värde som det är högst sannolikhet att bli. Som exempel tar vi en titt på illustrationerna nedan.
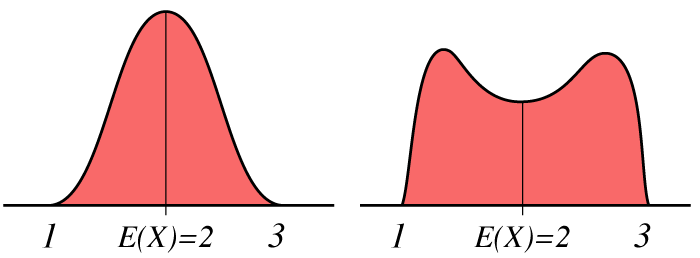
Väntevärdet kan jämföras med ett objekts tyngdpunkt och beräknas lite olika beroende på om man befinner sig i den kontinuerliga eller diskreta domänen. Väntevärdet tas med hänsyn till stokastiska variabler tex betecknas . Formel för väntevärdet är:
Men för att definiera ett intervall av de förväntade värdena som bör uppstå räcker det inte med väntevärdet självt.
Varians och standardavvikelse
Så som ovanstående illustration visar kan väntevärdet ge en ganska skev uppfattning om sannolikhetsfördelningen. Till detta används två spridningsmått som är väldigt lika, varians och standarsavvikelse.
Variansen beräknas genom:
När variansen är beräknad är det möjligt att ta fram standardavvikelsen med enkelhet genom:
Exercise
En s.v. har täthetsfunktionen . Beräkna väntevärdet och standarvvikelsen.
Solution
Vi beräknar variansen genom och börjar med att beräkna väntevärdet
för att sedan få fram . Vi fortsätter därefter med
Avslutningsvis beräknar vi väntevärdet och standardavvikningen
Kovarians
Kovarians är det första beroendemåttet som undersöker beroendet mellan två stokastiska variabler. Säg att vi har variablerna och , då betecknas kovariansen som . Värdet på kovariansen ger ett mått på korrelationen, ju högre värde ju starkare relation. Formeln för kovariansen ges av
Det är väldigt viktigt att inse att korrelationsvärdet innebär att och är okorrelerade. Däremot behöver detta nödvändigtvis inte innebära att de är oberoende. Om de däremot är korrelerade så måste de vara beroende.
Korrelationskoefficient
Korrelationskoefficienten är det andra beroendemåttet i kursen. Den kan betraktas som kovariansen utslagen över standardavvikningen som leder till att är begränsad mellan värdet och så att . Korrelationskoefficienten ges av
I denna mening kan korrelationskoefficienten betraktas som ett renare mått än kovariansen då det medför en tydligare tolkningsförmåga av det faktiska resultatet. Då anses variablerna okorrelerade medan då eller anses de vara korrelerade. Skillnaden mellan och är att motsvarar ett perfekt positivt linjär korrelation medan motsvarar ett perfekt negativt linjär korrelation.
Linjärtransform
Säg att vi vill ta reda på väntevärdet av en sammansatt s.v. , då är det viktigt lära sig dela upp uppgiften i delproblem genom linjärtransform. Det finns regler för väntevärde, varians och standardavvikning och de är:
Exercise
De s.v. och har standardavvikelserna och respektive. Deras kovarians är . Beräkna .
Solution
Vi har att:
Vi börjar med att dela upp variansutrycket
Vi beräknar nu variansen genom de givna standardavvikelserna:
Avslutningsvis får vi
Stora talens lag
Stora talens lag lyder: Om vi har en följd S.V. som är oberoende med har samma sannolikhetsfördelning och väntevärde kommer medelvärdet av dessa att närma sig väntevärdet så att förutsatt att antalet variabler är tillräckligt stort.
Som ett exempel kan vi tänka oss att vi har en korthög med kort från till som vi drar ett kort från, antecknar resultatet, och lägger tillbaka kortet samt blandar kortleken. Säg att vi gör denna dragning ett stort antal gånger, till exempel gånger. Vid ett sådant antal dragningar så kommer stora talens lags effekter visa sig.
Om varje enstaka dragning betraktas som en S.V. är väntevärdet densamma för samtliga alla variabler, och därmed, alla dragningar så att .
Stora talens lag säger att om vi gör denna dragning tillräckligt många gånger kommer medelvärdet av dragningarna att närma sig väntevärdet, i detta fall , oavsett vad korten faktiskt visar vid dragningen!