För att kunna med enkelhet tala och beräkna på sannolikhetsbaserade förlopp behövs först ett antal begrepp definieras.
Utfallsrum
Ett utfall är det direkta resultat vi kan observera från en sannolikhetsbaserad situation. Ett utfallsrum är mängden av alla möjliga utfall som kan uppstå. Utfallsrummet betecknas med medan individuella utfall betecknas med . Notera att utfallsrummet inte har något att göra med vad den faktiska sannolikheten för varje värde att uppstå, den snarare beskriver alla värden som kan uppstå.
Ett exempel på en sannolikhetsbaserad situation är ett tärningskast. Talet som tärningen visar vid kast är utfallet så som medan utfallsrummet är alla värden som kan uppstå vid utfall, i detta fall .
Händelse
En händelse är en samling av en eller flera utfall så att . Om någon utav är ett utfall som uppstår anses alltså händelsen ha inträffat.
För att jämföra med ovanstående tärningsexempel skulle en händelse kunna vara . De gånger tärningen visar eller vid tärningskast har alltså händelsen inträffat.
Händelsemängder
Union och Snitt
Säg att vi har två olika händelser och som har en del utfall gemensamt men inte alla (t.ex. ). I det fallet kan det vara intressant att prata om två nya typer av händelser:
Händelsen som uppstår då och inträffar samtidigt, uttalas snittet.
Händelsen som uppstår då eller eller både och inträffar, uttalas unionen.
Om så skulle snittet av händelserna vara medan unionen av händelserna vara
Disjunkta händelser och den tomma mängden
Om vi istället har två händelser och som inte har några utfall gemensamt alls, så som , skulle de då vara disjunkta. Händelsen att båda inträffar samtidigt blir följaktligen tom på utfall och kallas därför den tomma mängden som betecknas med så att: .
Komplementhändelse
Om vi istället har en händelse så kan dess komplementära händelse betecknas som innehåller alla utfall som inte innehåller.
Om vi har utfallsrummet och händelsen är definieras som blir då komplementhändelsen
Sammanfattning
Alla dessa olika händelser kan illustreras så att utfallsrummet är en yta där händelserna och är en del av denna yta.
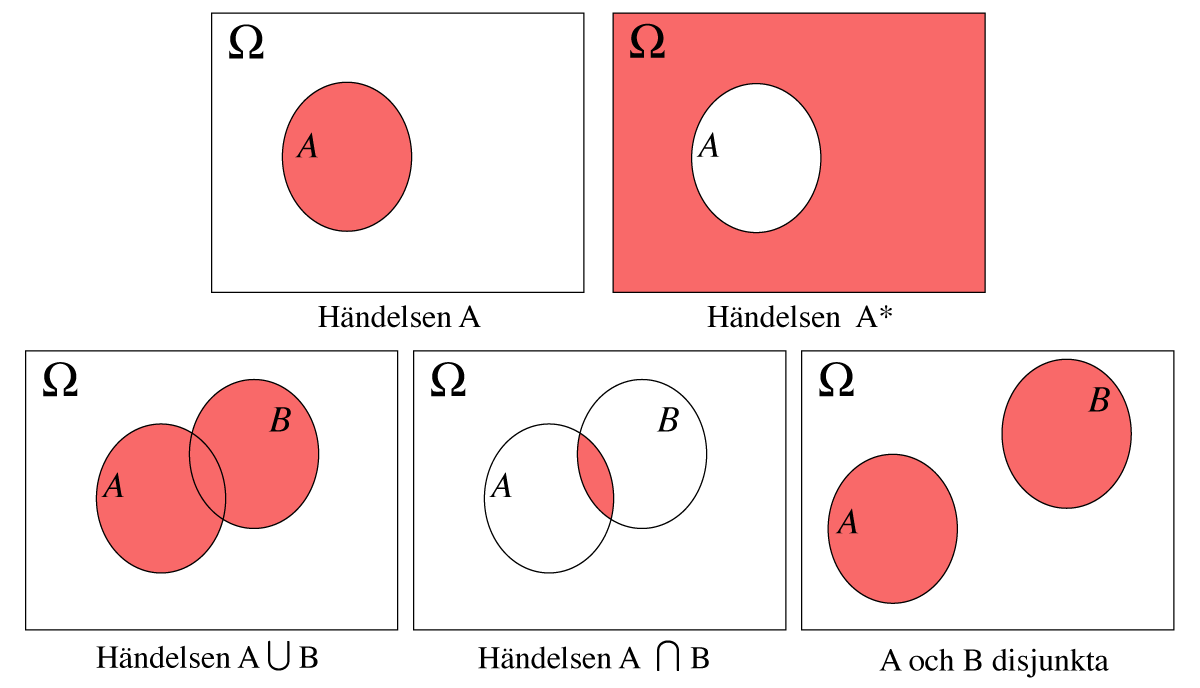
Sannolikhet
Sannolikheter definieras med avseende på händelser. Om vi vill veta vad sannolikheten för händelsen att inträffa betecknas det . Säg istället att vi har två händelser och söker sannolikheten för att både inträffar samtidigt (alltså snittet), då betecknas det . Sambandet mellan att händelserna inträffar samtidigt och att någon av händelserna (unionen) inträffar ges av följande formel.
Kombinatorik
För att kunna behandla repeterande sannolikhetsbaserade förlopp krävs kännedom om kombinatorik. Det som i huvudsakligen är intressant är att beräkna antalet gynnsamma kombinationer (som satisfierar det som efterfrågas) och antalet möjliga kombinationer. Med dessa kan man beräkna sannolikheten för att händelsen inträffar genom
För att kunna beräkna dessa behöver vi känna till hur kombinationerna tillkommer. Det finns fyra olika vis vi kan utföra en dragning på. Vi kan ta hänsyn till ordningen utfallen kommer i och så kan vi efter varje dragning lägga tillbaka det dragna utfallet. Totalt sett ger detta oss dessa olika dragningstekniker.
Med hänsyn till ordning, med återläggning.
Utan hänsyn till ordning, med återlämning.
Med hänsyn till ordning, utan återläggning.
Utan hänsyn till ordning, utan återläggning.
Alla dessa olika dragningstekniker kräver olika beräkningar för att beräkna antalet kombinationer eller antalet utfall som kan uppstå. Antalet möjliga sätt det går att dra element ur en population av element ges av:
Där över ges av
Miniräknartips: För att beräkna med enkelhet på grafräknaren så använd som finns på MATH.
Metoden för att beräkna sannolikhet genom kombinatorik har ett annorlunda tankesätt. Tanken är att man använder formlerna för att beräkna både de gynnsamma fallen och de möjliga fallen. För att ge klarhet till dessa formler tänker vi oss ett exempel med en urna.
Exercise
Vi har en urna med kulor varav är vita, är svarta och är gråa. Nu drar vi kulor. Vad är sannolikheten att vi får gråa kulor och svarta om vi inte tar hänsyn till ordning och inte använder återläggning?
Solution
Först beräknar vi de möjliga fallen. Dessa ges av att sätta och samt beräkna .
Nu beräknar vi de gynnsamma fallen genom att tänka att vi delar in kulorna i tre olika högar efter färg. Först tar vi reda på hur många kombinationer vi kan dra gråa kulor ur en hög av gråa kulor genom att beräkna .
Vi har nu dragit av gånger och har därför dragningar kvar att utföra. Vi tar nu reda på antalet kombinationer ur högen med svarta kulor. Detta ger oss
Vi beräknar nu det totala antalet gynnsamma fall genom att multiplicera de gynnsamma kombinationerna vi fått från beräkning med varje hög
Avslutningen dividerar vi de gynnsamma fallen med de möjliga och får sannolikheten
Sannolikheten att dra gråa kulor och svarta är alltså
Betingad sannolikhet
Säg att vi har händelserna och som har ett beroende; om inträffar förändras sannolikheten för att ska inträffa. I sannolikhetsläran kallas detta sannolikheten för betingat och betecknas . Sambandet mellan betingat och hur händelser vanligtvis inträffar ges av formeln
Komplementhändelsen till ges av
Exercise
Sannolikheten att en student går på torsdagspuben är
Sannolikheten att en student går på puben och skolkar är
Vad är sannolikheten att studenten kommer att skolka på fredagens morgonföreläsning givet att den var på torsdagspuben?
Solution
Vi har att
Vi söker och beräknar det genom
Detta innebär att det finns en risk att studenten missar morgonföreläsningen dagen efter en torsdagspub om uppgiftens antaganden är korrekta. Huruvida detta stämmer överens med verkligheten lämnas till läsaren att undersöka.
Det finns även en mera omfattande formler som beskriver förhållandet mellan och som ges av
Baye's sats
Säg att vi har flera händelser och . Säg också att alla händelser där är disjunkta och tillsammans utgör hela utfallsrummet .
Då kan vi använda Baye's sats i samband med betingad sannolikhet för att till exempel beräkna då vi har . Bayes sats har följande utseende.
Lagen om total sannolikhet
Nämnaren i Baye's sats är speciell. Den är i själva verket en av sannolikhetsteoriens mest etablerade satser – Lagen om total sannolikhet. Den säger att om vi har flera disjunkta händelser som tillsammans utgör ett utfallsrum så kan till exempel sannolikheten av en annan händelse beräknas då vi har . Satsen ser ut såhär och motsvarar nämnaren i förra formeln.
Exercise
Vi har att:
Sannolikheten att studenter är på borggården givet att solen skiner är
Sannolikheten att ingen student är på borggården givet att solen inte skiner är
Sannolikheten att solen skiner är
Vad är sannolikheten att solen skiner givet att studenter är på borggården?
Solution
Vi har givet att:
Vi vill beräkna . Detta kan vi göra genom lagen om total sannolikhet eller Bayes sats och därför gör både och! Vi börjar med Bayes sats då det är den enklaste lösningen.
Bayes sats
För att ta reda på ställer vi upp bayes sats för detta problem
Vi sätter in siffrorna och får det till
Lagen om total sannolikhet
Vi beräknar genom
Vi beräknar därför genom betingat-sambandet
och därefter genom lagen om total sannolikhet
Avslutningsvis beräknar vi
Oberoende händelser
Oberoende händelser är händelser som genuint inte har något med varandra att göra, det vill säga, händelser där sannolikheten att en händelse inträffar givet att händelse har inträffat är . Det vill säga, att inte på något vis förändrar sannolikheten att inträffar. Oberoende händelser medför därmed följande för händelserna och
Oberoende vs disjunkta händelser
Notera att begreppet oberoende inte är på något vis relaterat till att händelserna är disjunkta. För att göra detta tydligt säger vi att vi har två händelser och .
När två händelser är oberoende så måste de vara från olika utfallsrum, alltså att och där utfallsrummen är olika som till exempel. .
När två händelser är disjunkta kommer de från samma utfallsrum men inte innehåller samma utfall, dvs . Om till exempel så kan händelserna vara och för att de ska vara disjunkta.
Anledningen till att en händelse inte kan vara både disjukt och oberoende relativt en annan händelse är att inte kan både ha samma utfallsrum som samtidigt som den har sitt eget utfallsrum.
Exercise
Vi har händelserna och . Nedan ges sannolikheter för varje händelse att inträffa.
Avgör om händelserna är oberoende då .
Solution
Vi vill kontrollera om och gör detta genom att börjar med att ta redan på vad med formeln
Vi använder detta resultat för att beräkna som ges av
Då vet vi att händelserna är oberoende.