Inledning
Denna lektion går igenom tre funktioner som har en central del i sannolikhetsläran. De två första av dessa beskriver likartade saker i olika domäner, ena för den diskreta och den andra för den kontinuerliga domänen. Den tredje är ett en förlängning av de båda och kan appliceras på båda domänerna.
En del utfallsvärden av stokastiska variabler förekommer vanligen oftare än andra. I verkligheten är det väldigt sällan att samtliga utfall av en händelse inträffar med lika stor sannolikhet. Allt är inte ett tärningskast under ideella förhållanden. Av denna anledning är det viktigt att inse att det finns olika sannolikhetsfördelningar som beskriver hur sannolikheten är fördelad över utfallen. Denna fördelning varierar beroende på typen av händelse.
Innan man kan beskriva sannolikhetsfördelningar är det viktigt att veta om utfallsrummet är diskret eller kontinuerligt. Om den är diskret används beskrivs fördelningen med sannolikhetsfunktionen medan om den är kontinuerlig beskrivs den med täthetsfunktionen.
Sannolikhetsfunktion
För att kunna beskriva sannolikhetsfördelningar myntas ett begrepp unikt för det diskreta fallet: Sannolikhetsfunktionen . Med denna funktion given går det att se hur sannolikheten beror på utfallsvärden där värdet på sannolikhetsfunktionen ger sannolikheten att det värdet uppstår, därmed .
För att knyta an till tidigare exempel med tärningskast visar det sig att ett tärningskast under ideella förhållanden inte beror på utfallsvärdet alls, sannolikheten är alltid oavsett vilket värde tärningen visar. För utfallet skrivs blir alltså sannolikheten . Fördelningen är alltså väldigt platt och jämnt fördelad över utfallen.
Säg att tärningen har ett fabriksfel och är obalanserad kommer detta ge en annan sannolikhetsfördelning vilket resulterar i att en del värden uppträder oftare än andra. För att kunna visualisera sannolikhetsfunktionen i såna fall kan man tänka sig ett antal staplar, en för varje utfallsvärde, där varje stapels area representerar sannolikheten för dess utfallsvärde. För en obalanserad tärning med störst chans att få och därefter och minst chans att få kan sannolikhetsfördelningen illustreras såhär
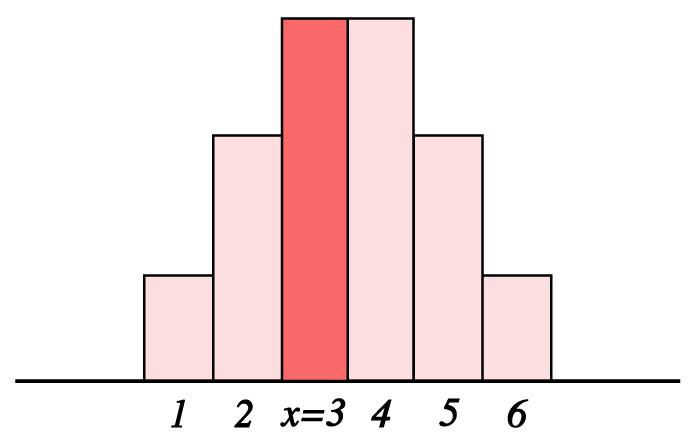
Om vi skulle beräkna skulle alltså det ge oss arean för den markerade stapeln.
Exercise
Vi har den diskreta sannolikhetsfördelningen som ges av sannolikhetsfunktionen
Beräkna sannolikheten .
Solution
Då är sannolikheten för att vi får ett utfall med värdet eller beräknar vi varje utfalls sannolikhet att uppstå och adderar deras sannolikheter därefter, alltså . Vi får att
Detta ger oss
Vidare till nästa funktion som gäller för det kontinuerliga fallet - Täthetsfunktionen!
Täthetsfunktion
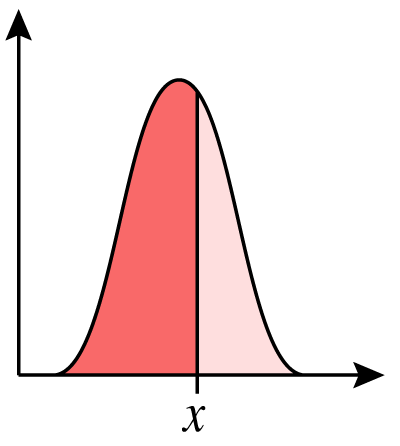
För det kontinuerliga utfallsrum och stokastiska variabler används täthetsfunktionen för att beskriva sannolikhetsfördelningen. Täthetsfunktionen mäter sannolikhetsdensiteten alltså hur tätpackad sannolikheten är under angivet område. I detta fall är sannolikheten arean under funktionen. Detta betyder två saker.
För det första kan vi inte längre tänka att ett specifikt utfall har en sannolikhet . Anledningen till det är att ett specifikt utfall är en punkt och arean under en punkt är noll.
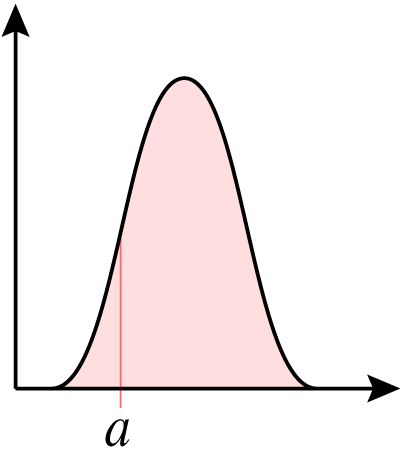
Vi måste istället tänka att vi vill mäta sannolikheten för ett intervall av utfallsvärden där vi integrerar över detta intervall för att ta reda på arean och sannolikheten.
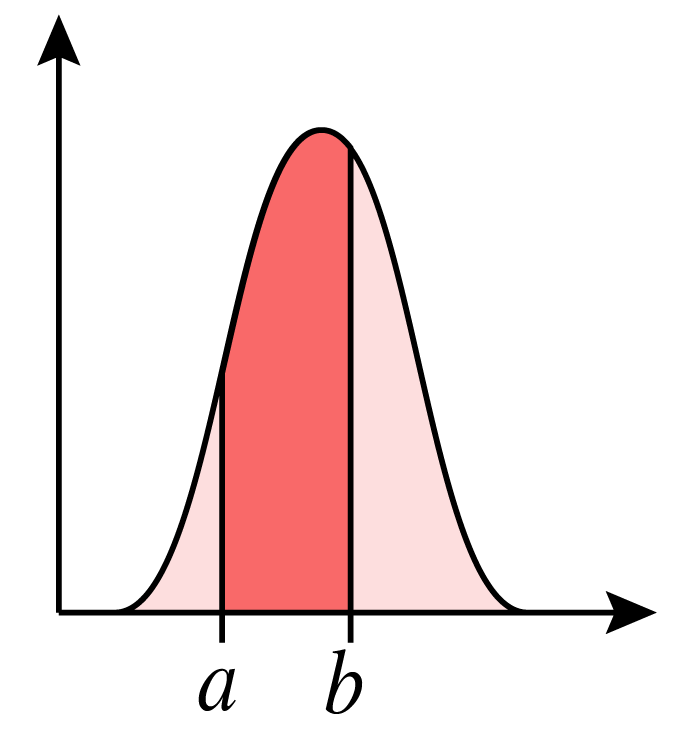
Sambandet mellan täthetsfunktion och sannolikhet blir därför
Avslutningsvis kommer vi prata om en ytterligare funktion som också används för att beräkna sannolikhet för intervall av utfall, dock för både det diskreta och kontinuerliga fallet.
Exercise
Vi har den kontinuerliga sannolikhetsfördelningen
Beräkna
Solution
Då vi inom intervallet är över noll vet vi att . För att ta reda på sannolikheten integrerar vi med som undre gräns och som övre gräns. Att det står i intervallet spelar ingen roll och kan antas som . Detta så arean under en punkt är noll. Vi beräknar integralen
som också motsvarar .
Fördelningsfunktion
Fördelningsfunktionen skrivs är ännu en funktion som beskriver sannolikhetsfördelningar genom intervall. Formellt beskrivs fördelningsfunktionen som . Med detta utgår fördelningsfunktionen med att värdet är den övre gränsen för intervallet.
Diskreta fallet
För diskreta sannolikhetsfördelningar med sannolikhetsfunktionen blir fördelningsfunktionen summan av de som intervallet omfattar. Anledningen till att vi infört ett är för att numera är den övre gränsen för intervallet medan är värdet på stokastiska variabeln . Fördelningsfunktionen beskrivs alltså i det diskreta fallet som
För att jämföra med det tidigare illustration av tärningskast skulle motsvara
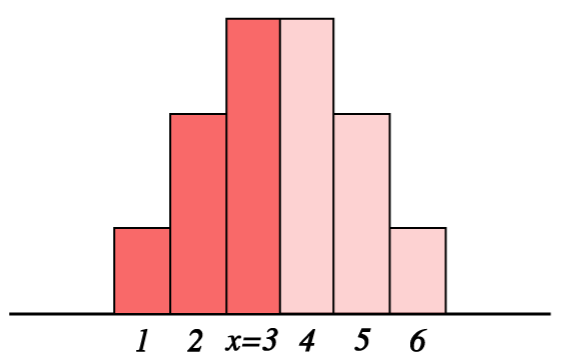
Detta då .
Kontinuerliga fallet
För det kontinuerliga fallet beskrivs fördelningsfunktionen enklast som integralen av täthetsfunktionen med som övre gräns. Alltså
I detta fall är värdet på den stokastiska variabeln och den övre gräns på integralen. Detta kan då illustreras som