Vad är en derivata?
Derivator används framförallt för att mäta förändringen av en funktion. Derivatan till funktionen betecknas antingen (läses "f prim av x") eller (läses "df, dx").
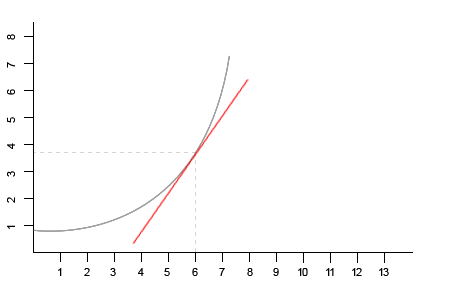
På bilden nedan ser ni kurvan till funktionen . Den röda linjen är tangenten till kurvan vid . Ur ett geometriskt perspektiv är derivatan till i detsamma som riktningskoefficienten till kurvans tangent vid .
Strikt definition
Derivatans strikta definition används sällan i uträkningar, men ibland måste man rabbla upp den på tentan för att visa att man kan den.
Derivatan till funktionen i punkten definieras som:
Om gränsvärdet existerar i en punkt säger man att " är deriverbar i punkten ".
Om det existerar ett gränsvärde för varje punkt i funktionens definitionsmängd säger man att " är deriverbar".
Deriveringsformler
Här nedanför ser ni en tabell med de vanligaste funktionerna och deras derivata . Dessa måste man lära sig utantill!
| Funktion f(x) | Derivata f′(x) |
|---|---|
| (konstant) | |
Uppgift
Räkna ut derivatan till funktionen
Lösning
Vi har tre stycken termer: , och .
Vi deriverar dem en i taget:
Derivatan till är (se i tabellen)
Derivatan till är (se i tabellen)
Derivatan till är noll eftersom det är en konstant! (se i tabellen)
Vi får alltså att derivatan till funktionen är:
OBS! Om du skulle råka glömma en deriveringsformel kan du enkelt komma tillbaka till den här sidan genom att gå in på: http://derivator.se! :-)